
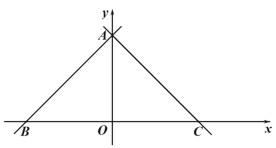
【題目】如圖,在平面直角坐標系,點 O 是原點,直線 y x 6分別交 x 軸,y 軸于點 B,A,經過點 A 的直線 y x b 交 x 軸于點 C.
(1)求 b 的值 ;
(2)點 D 是線段 AB 上的一個動點,連接 OD,過點 O 作 OE⊥OD 交 AC 于點 E,連接DE,將△ODE 沿 DE 折疊得到△FDE,連接 AF.設點 D 的橫坐標為 t,AF 的長為 d,當t> 3 時,求 d 與 t 之間的函數關系式(不要求寫出自變量 t 的取值范圍);
(3)在(2)的條件下,DE 交 OA 于點 G,且 tan∠AGD=3.點 H 在 x 軸上(點 H 在點O 的右側),連接 DH,EH,FH,當∠DHF=∠EHF 時,請直接寫出點 H 的坐標,不需要寫出解題過程.
【答案】(1)b=6;(2)d=6+2t;(3)H點的坐標為(2,0)或(10,0).
【解析】
(1)由y=x+6求得A點坐標,再將A點坐標代入y=x+b中,便可求得b;
(2)過點D分別作DM⊥x軸于點M,DN⊥y軸于點N,過點F作FR⊥AF交AE于點R,可證明四邊形DMON為矩形,再證△AOD≌△COE(ASA),用t表示AD,然后證明△ADF≌△REF(AAS),進而用t表示AR,問題便可迎刃而解;
(3)分兩種情況解答:第一種情況,當FH平分∠DHE時,連接OF,過E作EK⊥x軸于點K,作EL⊥y軸于點L,設正方形ODFE的外接圓交x軸于點H,證明△ODM≌△EOK(AAS),用t表示出EL,OL,再由tan∠AGD=3,便可用t表示GN,GL,由OA=6列出t的方程求得t,便可求得H點坐標;第二種情況,當∠DHF與∠EHF重合時,延長DE與x軸交于點H,求出DE與x軸的交點坐標便可.
解:(1)令x=0,得y=x+6=6,
∴A(0,6),
把A(0,6)代入y=x+b中,得b=6;
(2)令y=0,得y=x+6=0,則x=6,
∴B(6,0),
∵點D的橫坐標為t,
∴D(t,t+6),
令y=0,得y=x+6=0,x=6,
∴C(6,0),
∵OA=OB=6,
∴∠OAB=∠OBA=45°,
同理∠OAC=∠OCA=45°,
∴∠BAC=90°,
在Rt△AOC中,AC=![]() OA=
OA=![]() ,
,
如圖1,過點D分別作DM⊥x軸于點M,DN⊥y軸于點N,
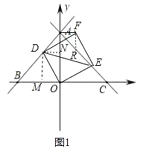
∵∠DMO=∠MON=∠OND=90°,
∴四邊形DMON為矩形,
∴DN=OM=t,
在Rt△ADN中,∠DAN=45°,AD=![]() ,
,
∵∠AOD+∠AOE=90°,∠COE+∠AOE=90°,
∴∠AOD=∠COE,
又∵∠OAD=∠OCE=45°,OA=OC,
∴△AOD≌△COE(ASA),
∴OD=OE,AD=CE=![]() ,
,
∵△DFE和△DOE關于DE對稱,
∴DF=OD=OE=EF,∠DFE=∠DOE=90°,
過點F作FR⊥AF交AE于點R,
∵∠AFD+∠DFR=90°,∠RFE+∠DFR=90°,
∴∠AFD=∠RFE,
∵∠ERF=∠RAF+∠AFR=∠RAF+90°,∠DAF=∠RAF+∠DAR=∠RAF+90°,
∴∠ERF=∠DAF,
∴△ADF≌△REF(AAS),
∴AF=RF,AD=RE=![]() ,
,
∴∠FAR=∠FRA,
又∵∠FAR+∠FRA═90°,
∴∠FAR=∠FRA=45°,
在Rt△AFR中,AR=ACCEER=![]() ,AF=
,AF=![]() AR=6+2t,
AR=6+2t,
∴d=6+2t;
(3)如圖2,連接OF,過E作EK⊥x軸于點K,,作EL⊥y軸于點L,
由(2)可得四邊形ODFE是正方形,設正方形ODFE的外接圓交x軸于點H,
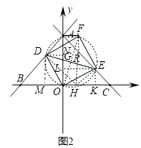
∴∠DOM+∠ODM=∠DOM+∠EOK=90°,
∴∠ODM=∠EOK,
∵∠OMD=∠EKO=90°,OD=EO,
∴△ODM≌△EOK(AAS),
∴EK=OM=DN=OL=t,LE=OK=DM=6+t,
∵tan∠AGD=3,DN=t,
∴![]() ,即
,即![]() ,
,
∴GN=![]() ,GL=
,GL=![]() ,
,
∴OA=OL+GL+GN+AN=![]() ,
,
∵OA=6,
∴2t+2=6,
∴t=2,
∴AF=6+2t═2,
∵OF是正方形ODFE的外接圓的直徑,
∴FH⊥x軸,∠DHF=∠DOF=∠EOF=45°=∠EHF,
∴H(2,0)滿足條件;
如圖3,延長DE與x軸交于點H,則∠DHF=∠EHF,
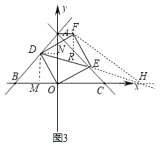
由以上知D(2,4),E(4,2),
設直線DE的解析式為:y=kx+b(k≠0),
則![]() ,解得:
,解得: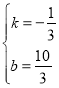 ,
,
∴直線DE的解析式為:![]() ,
,
當y=0時,得![]() ,
,
解得:x=10,
∴H(10,0),
綜上,H點的坐標為(2,0)或(10,0).


科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,一次函數![]() (a,b為常數,且
(a,b為常數,且![]() )與反比例函數
)與反比例函數![]() (m為常數,且
(m為常數,且![]() )的圖象交于點A(﹣2,1)、B(1,n).
)的圖象交于點A(﹣2,1)、B(1,n).

(1)求反比例函數和一次函數的解析式;
(2)連結OA、OB,求△AOB的面積;
(3)直接寫出當![]() 時,自變量x的取值范圍.
時,自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
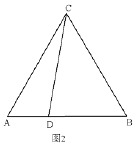
【題目】已知![]() 為等邊三角形,點
為等邊三角形,點![]() 是線段
是線段![]() 上一點(不與
上一點(不與![]() ,
,![]() 重合).將線段
重合).將線段![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到線段
得到線段![]() ,連結
,連結![]() ,
,![]() .
.
(1)依題意補全圖1并判斷![]() 與
與![]() 的數量關系.
的數量關系.
(2)過點![]() 作
作![]() 交
交![]() 延長線于點
延長線于點![]() ,用等式表示線段
,用等式表示線段![]() ,
,![]() 與
與![]() 之間的數量關系并證明.
之間的數量關系并證明.
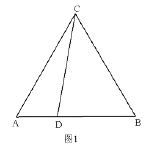
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠DAC是△ABC的一個外角.
實驗與操作:根據要求進行尺規作圖,并在圖中標明相應字母(保留作圖痕跡,不寫作法)
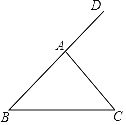
(1)作∠DAC的平分線AM;
(2)作線段AC的垂直平分線,與AM交于點F,與BC邊交于點E,連接AE、CF
探究與猜想:若∠BAE=36°,求∠B的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖 1、圖 2 均是 6×6 的正方形網格,每個小正方形的頂點稱為格點,小正方形的邊長為 1,點 A、B、C、D 均在格點上.在圖 1、圖 2 中,只用無刻度的直尺,在給定的網格中按要求畫圖,所畫圖形的頂點均在格點上,不要求寫出畫法.
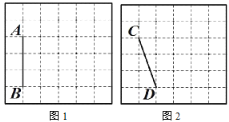
(1)在圖 1 中以線段 AB 為邊畫一個△ABM,使∠ABM=45°,且△ABM 的面積為 6;
(2)在圖 2 中以線段 CD 為邊畫一個四邊形 CDEF,使∠CDE=∠CFE=90°,且四邊形 CDEF 的面積為 8.
查看答案和解析>>
科目:初中數學 來源: 題型:
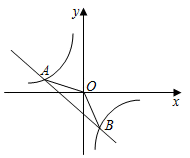
【題目】如圖,一次函數y=﹣x+b的圖象與反比例函數y=![]() 的圖象交于A、B兩點,且A點坐標為(﹣2,1),一次函數交x軸于點C.
的圖象交于A、B兩點,且A點坐標為(﹣2,1),一次函數交x軸于點C.
(1)試確定上述反比例函數和一次函數的表達式;
(2)求△AOB的面積;
(3)直接寫出使反比例函數大于一次函數的x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() .請按照要求寫出符合條件的拋物線的解析式.
.請按照要求寫出符合條件的拋物線的解析式.
(1)若拋物線![]() 與
與![]() 關于
關于![]() 軸對稱,則
軸對稱,則![]() = ;
= ;
(2)若拋物線![]() 與
與![]() 關于
關于![]() 軸對稱,則
軸對稱,則![]() = ;
= ;
(3)若拋物線![]() 與
與![]() 關于坐標原點對稱,則
關于坐標原點對稱,則![]() = ;
= ;
(4)若拋物線![]() 是由
是由![]() 繞著點P(1,0)旋轉180°后所得,則
繞著點P(1,0)旋轉180°后所得,則![]() = .
= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年3月31日,以“雙城有愛,一生一世”為主題的鄭開馬拉松開賽.在這次馬拉松長跑比賽中,抽取了10名女子選手,記錄她們的成績(所用的時間)如下:
選手(序號) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
時間(分鐘) | 152 | 155 | 166 | 178 | 183 | 189 | 193 | 195 | 195 | 198 |
關于這組數據,下列說法不正確的是( )
A.這組樣本數據的中位數是186
B.這組樣本數據的眾數是195
C.這組樣本數據的平均數超過170
D.這組樣本數據的方差小于30
查看答案和解析>>
科目:初中數學 來源: 題型:
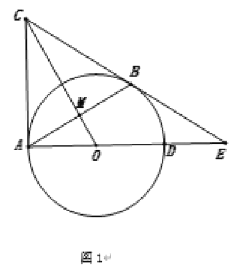
【題目】![]() 、
、![]() 為
為![]() 的切線,切點分別為點
的切線,切點分別為點![]() 、
、![]() ,延長
,延長![]() 交
交![]() 于點
于點![]() ,交
,交![]() 的延長線于點
的延長線于點![]() ,連接
,連接![]() 、
、![]() ,
,![]() 與
與![]() 交于點
交于點![]() .
.
(1)如圖1,求證:![]() ;
;
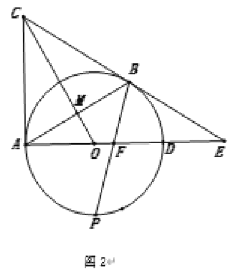
(2)如圖2,點![]() 是弧
是弧![]() 的中點,連接
的中點,連接![]() 交AD于點
交AD于點![]() ,求證:
,求證:![]() ;
;
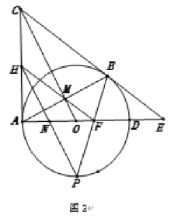
(3)如圖3,在(2)的條件下:連接![]() 并延長交
并延長交![]() 于點
于點![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() ,若
,若![]() ,
,![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com