
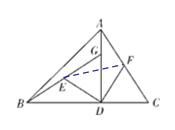
【題目】如圖,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分別是BG,AC的中點.
(1)求證:DE=DF,DE⊥DF;
(2)連接EF,若AC=10,求EF的長.

【答案】(1)證明見解析;(2)![]() .
.
【解析】試題分析:
(1)由已知條件先證△BDG≌△ADC,再證△BDE≌△ADF即可得到所求結論;
(2)如圖,由(1)可知∠ADC=90°,△DEF是等腰直角三角形, 結合F是AC的中點可得DF=![]() AC=5,這樣用勾股定理即可求得EF的長度.
AC=5,這樣用勾股定理即可求得EF的長度.
試題解析:
(1)∵AD⊥BC于點D,
∴∠BDG=∠ADC=90°.
∵BD=AD,DG=DC,
∴△BDG≌△ADC,
∴BG=AC.
∵E,F分別是BG,AC的中點,
∴DE=![]() BG,DF=
BG,DF=![]() AC.
AC.
∴DE=DF.
又∵BD=AD,BE=AF,
∴△BDE≌△ADF.
∴∠BDE=∠ADF.
∴∠EDF=∠EDG+∠ADF=∠EDG+∠BDE=∠BDG=90°.
∴DE⊥DF.
(2)如圖,連接EF,
∵AC=10,∠ADC=90°,
∴DE=DF=![]() AC=5.
AC=5.
又∵∠EDF=90°,
∴EF=![]() .
.


科目:初中數學 來源: 題型:
【題目】科學家在實驗中測得某微生物長約為0.0000035米,將0.0000035用科學記數法表示為( )
A.0.35×10 -5B.3.5×106C.3.5×10 -6D.0.35×105
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x,y的方程組![]() ,則下列結論中正確的是( )
,則下列結論中正確的是( )
①當a=5時,方程組的解是![]() ;
;
②當x,y的值互為相反數時,a=20;
③不存在一個實數a使得x=y;
④若![]() ,則a=2.
,則a=2.
A. ①②③④ B. ②③ C. ②③④ D. ②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,△ABC中, BD平分∠ABC,且與△ABC的外角∠ACE的角平分線交于點D.
(1)若![]() ,
,![]() ,求∠D的度數;
,求∠D的度數;
(2)若把∠A截去,得到四邊形MNCB,如圖②,猜想∠D、∠M、∠N的關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,點A、B的坐標分別為(1,4)和(3,0),點C是y軸上的一個動點,且A、B、C三點不在同一條直線上,當△ABC的周長最小時,點C的坐標是( )
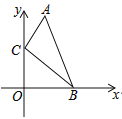
A. (0,0); B. (0,1); C. (0,2); D. (0,3).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于平面直角坐標系中的任意兩點P1(x1,y1),P2(x2,y2),我們把|x1-x2|+|y1-y2|叫做P1、P2兩點間的直角距離,記作d(P1,P2).
(1) 令P0(2,-3),O為坐標原點,則d(O,P0)= ;
(2)已知O為坐標原點,動點P(x,y)滿足d(O,P)=1,請寫出x與y之間滿足的關系式,并在所給的直角坐標系中畫出所有符合條件的點P所組成的圖形;
(3)設P0(x0,y0)是一定點,Q(x,y)是直線y=ax+b上的動點,我們把d(P0,Q)的最小值叫做P0到直線y=ax+b的直角距離. 若P(a,-3)到直線y=x+1的直角距離為6,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
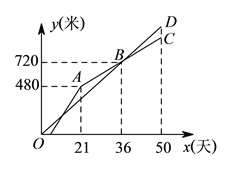
【題目】甲、乙兩個工程隊共同開鑿一條隧道,甲隊按一定的工作效率先施工,一段時間后,乙隊從隧道的另一端按一定的工作效率加入施工,中途乙隊遇到碎石層,工作效率降低,當乙隊完成碎石層時恰好隧道被打通,此時甲隊工作了![]() 天,設甲、乙兩隊各自開鑿隧道的長度為
天,設甲、乙兩隊各自開鑿隧道的長度為![]() (米),工作時間為
(米),工作時間為![]() (天),
(天),![]() 與
與![]() 之間的函數圖像如圖所示,下列說法:
之間的函數圖像如圖所示,下列說法:
①甲每天開鑿隧道![]() 米;
米;
②這條隧道總長為![]() 米;
米;
③當乙遇上碎石層時,甲恰好開鑿隧道![]() 米,
米,
④若乙在甲施工![]() 天后開始施工,則乙在遇到碎石層之前的施工速度比之后快
天后開始施工,則乙在遇到碎石層之前的施工速度比之后快![]() 米/天,其中正確的有__________.
米/天,其中正確的有__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小晗家客廳裝有一種三位單極開關,分別控制著A(樓梯)、B(客廳)、C(走廊)三盞電燈,在正常情況下,小晗按下任意一個開關均可打開對應的一盞電燈,既可三盞、兩盞齊開,也可分別單盞開.因剛搬進新房不久,不熟悉情況.
(1)若小晗任意按下一個開關,正好樓梯燈亮的概率是多少?
(2)若任意按下一個開關后,再按下另兩個開關中的一個,則正好客廳燈和走廊燈同時亮的概率是多少?請用樹狀圖或列表法加以說明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中AC平分∠BAD,∠ADC=∠ACB=90![]() ,E為AB的中點,AC與DE交于點F.
,E為AB的中點,AC與DE交于點F.

(1)求證: ![]() =AB·AD;
=AB·AD;
(2)求證:CE//AD;
(3)若AD=6, AB=8.求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com