
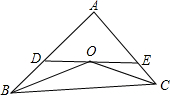
 如圖,在△ABC中,BO平分∠ABC,CO平分∠ACB,DE過O且平行于BC,已知△ADE的周長為10cm,BC的長為5cm,求△ABC的周長.
如圖,在△ABC中,BO平分∠ABC,CO平分∠ACB,DE過O且平行于BC,已知△ADE的周長為10cm,BC的長為5cm,求△ABC的周長.

 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案科目:初中數學 來源: 題型:
 如圖,在△ABC中,∠ACB=90°,AC=BC=1,取斜邊的中點,向斜邊作垂線,畫出一個新的等腰三角形,如此繼續下去,直到所畫出的直角三角形的斜邊與△ABC的BC重疊,這時這個三角形的斜邊為
如圖,在△ABC中,∠ACB=90°,AC=BC=1,取斜邊的中點,向斜邊作垂線,畫出一個新的等腰三角形,如此繼續下去,直到所畫出的直角三角形的斜邊與△ABC的BC重疊,這時這個三角形的斜邊為A、
| ||||
B、(
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com