
【題目】如圖,在菱形ABCD中,AB=BD,點(diǎn)E、F分別是線段AB、AD上的動點(diǎn)(不與端點(diǎn)重合),且AE=DF,BF與DE相交于點(diǎn)G.給出如下幾個結(jié)論:①△AED≌△DFB;②∠BGE大小會發(fā)生變化;③CG平分∠BGD;④若AF=2DF,則BG=6GF;![]() .其中正確的結(jié)論有_____(填序號).
.其中正確的結(jié)論有_____(填序號).
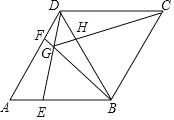
【答案】①③④.
【解析】
根據(jù)菱形的性質(zhì)得到AB=AD,推出△ABD為等邊三角形,得到∠A=∠BDF=60°,根據(jù)全等三角形的判定得到△AED≌△DFB;過點(diǎn)C作CM⊥GB于M,CN⊥GD于N(如圖1),根據(jù)全等三角形的性質(zhì)得到CN=CM,根據(jù)角平分線的定義得到CG平分∠BGD;過點(diǎn)F作FP∥AE交DE于P點(diǎn)(如圖2),根據(jù)平行線分線段成比例定理得到BG=6GF;推出B、C、D、G四點(diǎn)共圓,根據(jù)圓周角定理得到∠BGC=∠BDC=60°,∠DGC=∠DBC=60°,求得∠BGC=∠DGC=60°,過點(diǎn)C作CM⊥GB于M,CN⊥GD于N(如圖1),推出S四邊形BCDG=S四邊形CMGN,于是得到S四邊形CMGN=2S△CMG=2×![]() ×CG×
×CG×![]() CG=
CG=![]() CG2.
CG2.
解:①∵ABCD為菱形,
∴AB=AD,
∵AB=BD,∴△ABD為等邊三角形,
∴∠A=∠BDF=60°,
又∵AE=DF,AD=BD,
∴△AED≌△DFB(SAS),故本選項①正確;
②∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°,為定值,
故本選項②錯誤;
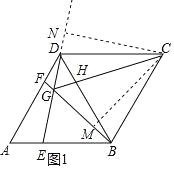
③過點(diǎn)C作CM⊥GB于M,CN⊥GD于N(如圖1),
則△CBM≌△CDN(AAS),
∴CN=CM,
∵CG=CG,
∴Rt△CNG≌Rt△CMG(HL),
∴∠DGC=∠BGC,
∴CG平分∠BGD;故本選項③正確;
④過點(diǎn)F作FP∥AE交DE于P點(diǎn)(如圖2),

∵AF=2FD,
∴FP:AE=DF:DA=1:3,
∵AE=DF,AB=AD,
∴BE=2AE,
∴FP:BE=FP:2AE=1:6,
∵FP∥AE,
∴PF∥BE,
∴FG:BG=FP:BE=1:6,
即BG=6GF,故本選項④正確;
⑤∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,
即∠BGD+∠BCD=180°,
∴點(diǎn)B、C、D、G四點(diǎn)共圓,
∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°,
∴∠BGC=∠DGC=60°,
過點(diǎn)C作CM⊥GB于M,CN⊥GD于N(如圖1),
則△CBM≌△CDN(AAS),
∴S四邊形BCDG=S四邊形CMGN,
S四邊形CMGN=2S△CMG,
∵∠CGM=60°,
∴GM=![]() CG,CM=
CG,CM=![]() CG,
CG,
∴S四邊形CMGN=2S△CMG=2×![]() ×CG×
×CG×![]() CG=
CG=![]() CG2,故本選項⑤錯誤;
CG2,故本選項⑤錯誤;
綜上所述,正確的結(jié)論有①③④,共3個,
故答案為①③④.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應(yīng)用題卡系列答案
口算與應(yīng)用題卡系列答案 名師點(diǎn)睛字詞句段篇系列答案
名師點(diǎn)睛字詞句段篇系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
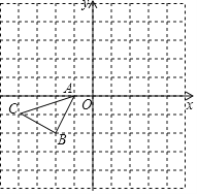
【題目】如圖,方格紙中的每個小正方形的邊長都為1,在建立平面直角坐標(biāo)系后,△ABC的頂點(diǎn)均在格點(diǎn)上.
(1)以點(diǎn)A為旋轉(zhuǎn)中心,將△ABC繞點(diǎn)A順時針旋轉(zhuǎn)90°得到△AB1C1,畫出△AB1C1;
(2)畫出△ABC關(guān)于原點(diǎn)O成中心對稱的△A2B2C2,若點(diǎn)B的坐標(biāo)為(-2,-2),則點(diǎn)B2的坐標(biāo)為_________.
(3)若△A2B2C2可看作是由△AB1C1繞點(diǎn)P順時針旋轉(zhuǎn)90°得到的,則點(diǎn)P的坐標(biāo)為______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
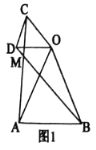
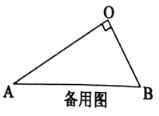
【題目】(1)問題發(fā)現(xiàn):
如圖1,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,連接
,連接![]() ,
,![]() 交于點(diǎn)
交于點(diǎn)![]() .
.
填空:①![]() 的值為 ;②
的值為 ;②![]() 的度數(shù)為 .
的度數(shù)為 .
(2)類比探究:如圖2,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,連接
,連接![]() 交
交![]() 的延長線于點(diǎn)
的延長線于點(diǎn)![]() .請求出
.請求出![]() 的值及
的值及![]() 的度數(shù),并說明理由;
的度數(shù),并說明理由;
(3)拓展延伸:在(2)的條件下,將![]() 繞點(diǎn)
繞點(diǎn)![]() 在平面內(nèi)旋轉(zhuǎn),
在平面內(nèi)旋轉(zhuǎn),![]() 、
、![]() 所在直線交于點(diǎn)
所在直線交于點(diǎn)![]() ,若
,若![]() ,
,![]() ,請直接寫出當(dāng)點(diǎn)
,請直接寫出當(dāng)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合時
重合時![]() 的長.
的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
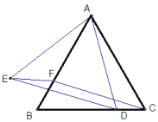
【題目】如圖,![]() 為等邊三角形,
為等邊三角形,![]() 、
、![]() 分別為
分別為![]() 、
、![]() 上的點(diǎn),且
上的點(diǎn),且![]() .
.
(1)求證:![]() ;
;
(2)以![]() 為邊作等邊三角形
為邊作等邊三角形![]() ,點(diǎn)
,點(diǎn)![]() 在線段
在線段![]() 上的何處時,四邊形
上的何處時,四邊形![]() 是平行四邊形且
是平行四邊形且![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
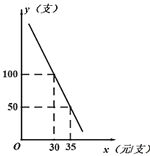
【題目】某網(wǎng)店專售一款電動牙刷,其成本為20元/支,銷售中發(fā)現(xiàn),該商品每天的銷售量y(支)與銷售單價x(元/支)之間存在如圖所示的關(guān)系.
(1)請求出y與x的函數(shù)關(guān)系式;
(2)該款電動牙刷銷售單價定為多少元時,每天銷售利潤最大?最大利潤是多少元?
(3)近期武漢爆發(fā)了“新型冠狀病毒”疫情,該網(wǎng)店店主決定從每天獲得的利潤中抽出 200 元捐贈給武漢,為了保證捐款后每天剩余利潤不低于550元,如何確定該款電動牙刷的售單價?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,拋物線y=﹣x2+mx+n交x軸于點(diǎn)A(﹣2,0)和點(diǎn)B,交y軸于點(diǎn)C(0,2).
(1)求拋物線的函數(shù)表達(dá)式;
(2)若點(diǎn)M在拋物線上,且S△AOM=2S△BOC,求點(diǎn)M的坐標(biāo);
(3)如圖2,設(shè)點(diǎn)N是線段AC上的一動點(diǎn),作DN⊥x軸,交拋物線于點(diǎn)D,求線段DN長度的最大值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
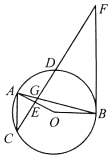
【題目】如圖,點(diǎn)A,B,C三點(diǎn)均在⊙O上,⊙O外一點(diǎn)F,有OA⊥CF于點(diǎn)E,AB與CF相交于點(diǎn)G,有FG=FB,AC∥BF.
(1)求證:FB是⊙O的切線.
(2)若tan∠F=![]() ,⊙O的半徑為
,⊙O的半徑為![]() ,求CD的長.
,求CD的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
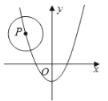
【題目】如圖,已知⊙P的半徑為4,圓心P在拋物線y=x2﹣2x﹣3上運(yùn)動,當(dāng)⊙P與x軸相切時,則圓心P的坐標(biāo)為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小明在一次用頻率估計概率的實(shí)驗中,統(tǒng)計了某一結(jié)果出現(xiàn)的頻率,并繪制了如圖所示的統(tǒng)計圖,則符合這一結(jié)果的實(shí)驗可能是( )
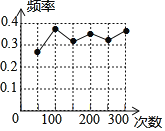
A.從分別寫著數(shù)字1,2,3的三個紙團(tuán)中隨機(jī)抽取一個,抽中2的概率
B.擲一枚質(zhì)地均勻的骰子,向上的點(diǎn)數(shù)是偶數(shù)的概率
C.同時拋擲兩枚質(zhì)地均勻的硬幣,一枚正面向上、一枚反面向上的概率
D.從一副去掉大小王的撲克牌,任意抽取一張,抽到紅桃的概率
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com