
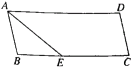
【題目】如圖,ABCD中,點E是CD延長線上一點,BE交AD于點F,DE=![]() CD.
CD.
(1)求證:△ABF∽△CEB
(2)若△DEF的面積為2,求ABCD的面積.
(3)若G、H分別為BF、AB的中點,AG、FH交于點O,求![]() .
.

【答案】(1)證明見解析;(2)24;(3)1:2.
【解析】
(1)由ABCD可知AB∥CD且∠BAD=∠C,據此可進行證明;
(2)先證明△DFD分別與△BAF、△EBC相似,利用相似比分別求出S△BFA和S梯形FDBC的面積;
(3)由G、H分別為BF、AB的中點可知GH為中位線,進而可證明△OHG∽△OAF并進行求解.
(1)證明:∵ABCD,
∴AB∥CE,AD∥BC,
∴∠ABF=∠E,
又∵ABCD是平行四邊形,
∴∠BAF=∠C,
△ABF∽△CEB,
(2)解:∵∠ABF=∠E,∠AFB=∠EFD,
∴△ABF∽△DEF,
∵AD∥BC,
∴△CEB∽△DEF,
∵DE=![]() CD,
CD,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵△DEF的面積為2,
∴S△BFA=8,S△EBC=18,
∴S梯形FDBC=18﹣2=16,
∴S平行四邊形ABCD=16+8=24,
(3)解:∵G、H為中點,
∴GH∥AF,2GH=AF,
∴OG:OA=HG:AF=1:2.


科目:初中數學 來源: 題型:
【題目】某商場計劃銷售甲、乙兩種產品共![]() 件,每銷售
件,每銷售![]() 件甲產品可獲得利潤
件甲產品可獲得利潤![]() 萬元, 每銷售
萬元, 每銷售![]() 件乙產品可獲得利潤
件乙產品可獲得利潤![]() 萬元,設該商場銷售了甲產品
萬元,設該商場銷售了甲產品![]() (件),銷售甲、乙兩種產品獲得的總利潤為
(件),銷售甲、乙兩種產品獲得的總利潤為![]() (萬元).
(萬元).
(1)求![]() 與
與![]() 之間的函數表達式;
之間的函數表達式;
(2)若每件甲產品成本為![]() 萬元,每件乙產品成本為
萬元,每件乙產品成本為![]() 萬元,受商場資金影響,該商場能提供的進貨資金至多為
萬元,受商場資金影響,該商場能提供的進貨資金至多為![]() 萬元,求出該商場銷售甲、乙兩種產品各為多少件時,能獲得最大利潤.
萬元,求出該商場銷售甲、乙兩種產品各為多少件時,能獲得最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方體的長為15,寬為10,高為20,點B離點C的距離為5,一只螞蟻如果要沿著長方體的表面從點A爬到點B,需要爬行的最短距離是__________

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,與
,與![]() 軸相交于點
軸相交于點![]() .
.

(1)求直線![]() 與坐標軸圍成的面積;
與坐標軸圍成的面積;
(2)在![]() 軸上一動點
軸上一動點![]() ,使
,使![]() 是等腰三角形;請直接寫出所有
是等腰三角形;請直接寫出所有![]() 點的坐標,并求出如圖所示
點的坐標,并求出如圖所示![]() 時點
時點![]() 的坐標;
的坐標;
(3)直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,與
,與![]() 軸相交于點
軸相交于點![]() ;點
;點![]() 是直線
是直線![]() 上一點,若
上一點,若![]() 的面積是
的面積是![]() 的面積的兩倍,求點
的面積的兩倍,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 一內角的平分線與邊相交并把這條邊分成2cm,3cm的兩條線段,求
一內角的平分線與邊相交并把這條邊分成2cm,3cm的兩條線段,求![]() 的周長.
的周長.
小華的解答過程如下:
如圖,![]() 平分
平分![]() 一內角
一內角![]() .
.
當![]() 時,∵
時,∵![]() 平分
平分![]() ,
,
∴![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() .∴
.∴![]() 的周長為
的周長為![]() .
.
你認為小華的解答過程對嗎?如果不對,請寫出正確的解答過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是![]() 的的直徑,BC
的的直徑,BC![]() AB于點B,連接OC交
AB于點B,連接OC交![]() 于點E,弦AD//OC,弦DF
于點E,弦AD//OC,弦DF![]() AB于點G.
AB于點G.
(1)求證:點E是![]() 的中點;
的中點;
(2)求證:CD是![]() 的切線;
的切線;

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC是邊長為3的等邊三角形,點D是邊BC上的一點,且BD=1,以AD為邊作等邊△ADE,過點E作EF∥BC,交AC于點F,連接BF,則下列結論中①△ABD≌△BCF;②四邊形BDEF是平行四邊形;③S四邊形BDEF=![]() ;④S△AEF=
;④S△AEF=![]() .其中正確的有( )
.其中正確的有( )

A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一水池中有水![]() ,如果每分鐘放出
,如果每分鐘放出![]() 的水,水池里的水量與放水時間有如下關系:
的水,水池里的水量與放水時間有如下關系:
放水時間(分) | 1 | 2 | 3 | 4 | … |
水池中水量 | 38 | 36 | 34 | 32 | … |
下列數據中滿足此表格的是( )
A.放水時間8分鐘,水池中水量![]() B.放水時間20分鐘,水池中水量
B.放水時間20分鐘,水池中水量![]()
C.放水時間26分鐘,水池中水量![]() D.放水時間18分鐘,水池中水量
D.放水時間18分鐘,水池中水量![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com