Question

【題目】如圖，直線y= x+ 與兩坐標軸分別交于A、B兩點．
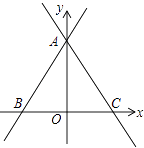
（1）求∠ABO的度數；
（2）過A的直線l交x軸半軸于C，AB=AC，求直線l的函數解析式．

Answer 1

【答案】
（1）解：對于直線y= x+ ，

令x=0，則y= ，

令y=0，則x=﹣1，

故點A的坐標為（0， ），點B的坐標為（﹣1，0），

則AO= ，BO=1，

在Rt△ABO中，

∵tan∠ABO= = ，

∴∠ABO=60°

（2）解：在△ABC中，

∵AB=AC，AO⊥BC，

∴AO為BC的中垂線，

即BO=CO，

則C點的坐標為（1，0），

設直線l的解析式為：y=kx+b（k，b為常數），

則 ，

解得： ，

即函數解析式為：y=﹣ x+

【解析】（1）根據函數解析式求出點A、B的坐標，然后在Rt△ABO中，利用三角函數求出tan∠ABO的值，繼而可求出∠ABO的度數；（2）根據題意可得，AB=AC，AO⊥BC，可得AO為BC的中垂線，根據點B的坐標，得出點C的坐標，然后利用待定系數法求出直線l的函數解析式．本題考查了待定系數法求一次函數解析式，涉及了的知識點有：待定系數法確定一次函數解析式，一次函數與坐標軸的交點，坐標與圖形性質，熟練掌握待定系數法是解答本題的關鍵．
【考點精析】解答此題的關鍵在于理解確定一次函數的表達式的相關知識，掌握確定一個一次函數，需要確定一次函數定義式y=kx+b（k不等于0）中的常數k和b．解這類問題的一般方法是待定系數法．