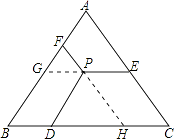
【題目】如圖，△ABC是等邊三角形，點P是三角形內(nèi)的任意一點，PD∥AB，PE∥BC，PF∥AC，若△ABC的周長為36，則PD+PE+PF=（ ）
A.12
B.8
C.4
D.3
【答案】A
【解析】解：如圖，延長EP、FP分別交AB、BC于G、H，則由PD∥AB，PE∥BC，PF∥AC，
∴四邊形PGBD和四邊形EPHC是平行四邊形，
∴PG=BD，PE=HC，
又△ABC是等邊三角形，
又有PF∥AC，PD∥AB可得△PFG，△PDH是等邊三角形，
∴PF=PG=BD，PD=DH，
又△ABC的周長為36，
∴PD+PE+PF=DH+HC+BD=BC= 
×36=12，
故A符合題意.
故答案為：A．
延長EP、FP分別交AB、BC于G、H，易證得四邊形PGBD、四邊形EPHC是平行四邊形以及△PFG、△PDH是等邊三角形，進(jìn)而根據(jù)三角形的周長可求得.
津橋教育計算小狀元系列答案科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，BE是線段AB的延長線，且∠CBE=∠A=∠C．
（1）由∠CBE=∠A可以判斷____∥_____，根據(jù)是_____________；
（2）由∠CBE=∠C可以判斷____∥_____，根據(jù)是_____________．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】我國邊防局接到情報，近海處有一可疑船只
正向公海方向航行，邊防部迅速派出快艇
追趕如圖1，圖2中
分別表示兩船相對海岸的距離
(海里)與追趕時間
(分)之間的關(guān)系.
根據(jù)圖象回答問題：
(1)哪條線表示到海岸的距離與追趕時間之間的關(guān)系？
(2)
哪個速度快？
(3)15分鐘內(nèi)能否追上？為什么？
(4)如果一直追下去，那么能否追上？
(5)當(dāng)逃離海岸12海里時，將無法對其進(jìn)行檢查，照此速度，能否在逃入公海前將其攔截？為什么？
(6)
與
對應(yīng)的兩個一次函數(shù)
與
中，
的實際意義各是什么？可疑船只與快艇的速度各是多少？
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，一次函數(shù)y＝kx＋b與反比例函數(shù)y＝
（x＞0）交于A（2，4），B（a，1），與x軸，y軸分別交于點C，D．
（1）直接寫出一次函數(shù)y＝kx＋b的表達(dá)式和反比例函數(shù)y＝
（x＞0）的表達(dá)式；
（2）求證：AD＝BC．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，ABCD中，AE平分∠BAD，交BC于E，DE⊥AE，下列結(jié)論：：①DE平分∠ADC；②E是BC的中點；③AD=2CD；④梯形ADCE的面積與△ABE的面積比是3：1，其中正確的結(jié)論的個數(shù)有（ ）
A.4
B.3
C.2
D.1
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
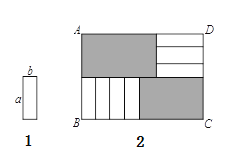
【題目】7張如圖的長為
，寬為
的小長方形紙片，按如圖的方式不重疊地放在矩形
內(nèi)，未被覆蓋的部分（兩個矩形）用陰影表示.設(shè)左上角與右下角的陰影部分的面積的差為
，當(dāng)
的長度變化時，則，
滿足（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，將△ABC繞點A順時針旋轉(zhuǎn)60°得到△ADE，點C的對應(yīng)點E恰好落在BA的延長線上，DE與BC交于點F，連接BD．下列結(jié)論不一定正確的是（ ）
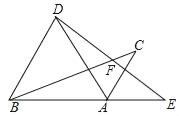
A. AD=BD B. AC∥BD C. DF=EF D. ∠CBD=∠E
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
