
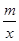 相交于C、D兩點,且點D的坐標為(1,6).
相交于C、D兩點,且點D的坐標為(1,6).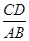 的值為 .
的值為 .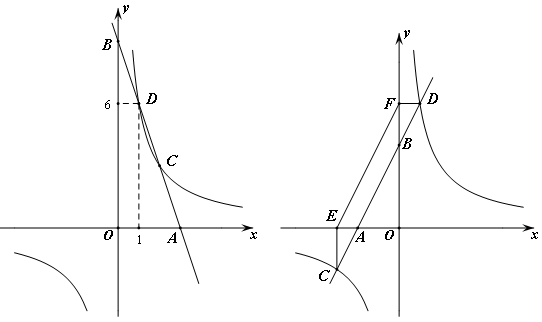
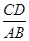 =2時,求tan∠OAB的值.
=2時,求tan∠OAB的值.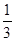 ,⑵①見解析②2
,⑵①見解析②2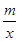 上,
上,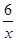 ,----------1分
,----------1分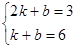 ,k=-3,b=9,故直線AB的解析式為y=-3x+9.-----3分
,k=-3,b=9,故直線AB的解析式為y=-3x+9.-----3分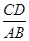 的值為
的值為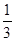 ----------------4分
----------------4分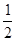 (-a)(-b)=
(-a)(-b)= 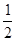 ab=3,----------------5分
ab=3,----------------5分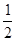 ×1×6=3,
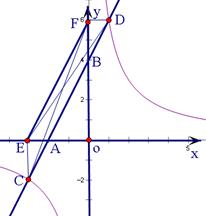
×1×6=3,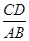 =2,設CD=2k,AB=k,DB=
=2,設CD=2k,AB=k,DB=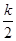 ,
,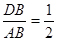 ,由ΔDFB∽ΔAOB,知OA=2,且
,由ΔDFB∽ΔAOB,知OA=2,且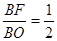 , -------10分
, -------10分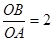 .------ ------11分
.------ ------11分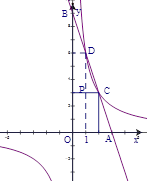


 能考試期末沖刺卷系列答案
能考試期末沖刺卷系列答案科目:初中數學 來源:不詳 題型:解答題
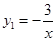 (x<0)的圖象相交于A點,與y軸、x軸分別相交于B、C兩點,且C(2,0),當
(x<0)的圖象相交于A點,與y軸、x軸分別相交于B、C兩點,且C(2,0),當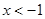 時,一次函數值大于反比例函數值,當
時,一次函數值大于反比例函數值,當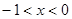 時,一次函數值小于反比例函數值.
時,一次函數值小于反比例函數值.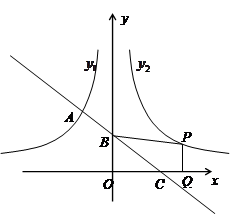
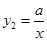 (x>0)的圖象與
(x>0)的圖象與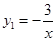 (x<0)的圖象關于y軸對稱,在
(x<0)的圖象關于y軸對稱,在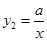 (x>0)的圖象上取一點P(P點的橫坐標大于2),過P點作PQ⊥x軸,垂足是Q,若四邊形BCQP的面積等于2,求P點的坐標.
(x>0)的圖象上取一點P(P點的橫坐標大于2),過P點作PQ⊥x軸,垂足是Q,若四邊形BCQP的面積等于2,求P點的坐標.查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
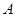 沿傾斜角為30°的山坡前進1500米到B,再次測得山頂D的仰角為60°,求山高CD. (結果保留根號)
沿傾斜角為30°的山坡前進1500米到B,再次測得山頂D的仰角為60°,求山高CD. (結果保留根號)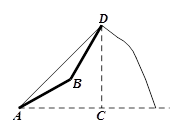 |
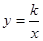 與直線
與直線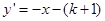 在第二象限的交點,AB⊥
在第二象限的交點,AB⊥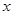 軸于B且S△ABO=
軸于B且S△ABO=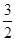 .
.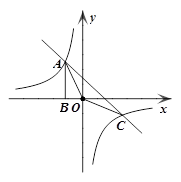
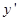 y.
y.查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
 交于A、B兩點, P是線段AB上的點(不與A、B重臺).過點A、B、P分別向x軸作垂線,垂足分別 為C、D、E,連接OA、OB、OP.設△AOC的面積為S1,△BOD的面積為S2,△POE的面積為S3,則( )
交于A、B兩點, P是線段AB上的點(不與A、B重臺).過點A、B、P分別向x軸作垂線,垂足分別 為C、D、E,連接OA、OB、OP.設△AOC的面積為S1,△BOD的面積為S2,△POE的面積為S3,則( )
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com