
【題目】如圖,在邊長為4的正方形ABCD中,點P在AB上從A向B運動,連接DP交AC于點Q.

(1)試證明:無論點P運動到AB上何處時,都有△ADQ≌△ABQ;
(2)當點P在AB上運動到什么位置時,△ADQ的面積是正方形ABCD面積的![]() ;
;
(3)若點P從點A運動到點B,再繼續在BC上運動到點C,在整個運動過程中,當點P運動到什么位置時,△ADQ恰為等腰三角形.
【答案】(1)證明見解析;(2)AP=2;(3)P在B點,C點,或在CP=4(![]() -1)處,△ADQ是等腰三角形.
-1)處,△ADQ是等腰三角形.
【解析】
試題分析:(1)可由SAS求得△ADQ≌△ABQ;
(2)過點Q作QE⊥AD于E,QF⊥AB于F,則QE=QF,若△ADQ的面積是正方形ABCD面積的![]() ,則有S△ADQ=
,則有S△ADQ=![]() ADQE=
ADQE=![]() S正方形ABCD,求得OE的值,再利用△DEQ∽△DAP有
S正方形ABCD,求得OE的值,再利用△DEQ∽△DAP有![]() ,解得AP值;
,解得AP值;
(3)點P運動時,△ADQ恰為等腰三角形的情況有三種:有QD=QA或DA=DQ或AQ=AD.由正方形的性質知,①當點P運動到與點B重合時,QD=QA,此時△ADQ是等腰三角形,②當點P與點C重合時,點Q與點C也重合,此時DA=DQ,△ADQ是等腰三角形,③當AD=AQ=4時,有CP=CQ,CP=AC-AD而由正方形的對角線的性質得到CP的值.
試題解析:(1)在正方形ABCD中,
無論點P運動到AB上何處時,都有
AD=AB,∠DAQ=∠BAQ,AQ=AQ,
∴△ADQ≌△ABQ;
(2)△ADQ的面積恰好是正方形ABCD面積的![]() 時,
時,
過點Q作QE⊥AD于E,QF⊥AB于F,則QE=QF,

∵在邊長為4的正方形ABCD中,
∴S正方形ABCD=16,
∴![]() AD×QE=
AD×QE=![]() S正方形ABCD=
S正方形ABCD=![]() ×16=
×16=![]() ,
,
∴QE=![]() ,
,
∵EQ∥AP,
∴△DEQ∽△DAP,
∴![]() ,即
,即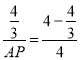 ,
,
解得AP=2,
∴AP=2時,△ADQ的面積是正方形ABCD面積的![]() ;
;
(3)若△ADQ是等腰三角形,則有QD=QA或DA=DQ或AQ=AD,
①當AD=DQ時,則∠DQA=∠DAQ=45°
∴∠ADQ=90°,P為C點,
②當AQ=DQ時,則∠DAQ=∠ADQ=45°,
∴∠AQD=90°,P為B,
③AD=AQ(P在BC上),
∴CQ=AC-AQ=![]() BC-BC=(
BC-BC=(![]() -1)BC
-1)BC
∵AD∥BC
∴![]() ,即可得
,即可得![]() =1,
=1,
∴CP=CQ=(![]() -1)BC=4(
-1)BC=4(![]() -1)
-1)
綜上,P在B點,C點,或在CP=4(![]() -1)處,△ADQ是等腰三角形.
-1)處,△ADQ是等腰三角形.


 七彩題卡口算應用一點通系列答案
七彩題卡口算應用一點通系列答案科目:初中數學 來源: 題型:
【題目】下列說法中,正確的個數為( )
①無限小數都是無理數;②不循環小數都是無理數;③無理數都是無限小數;④無理數也有負數;⑤無理數分為正無理數、零、負無理數.
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在信息快速發展的社會,“信息消費”已成為人們生活的重要部分.我市區機抽取了部分家庭,調查每月用于信息消費的金額,數據整理成如圖所示的不完整統計圖.已知A、B兩組戶數直方圖的高度比為1:5,請結合圖中相關數據回答下列問題:

(1)A組的頻數是 ,本次調查樣本的容量是 ;
(2)補全直方圖(需標明各組頻數);
(3)若該社區有1500戶住戶,請估計月信息消費額不少于300元的戶數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列每組數分別是三根小木棒的長度,用它們能擺成三角形的是( )
A. 3cm,4cm,8cm B. 8cm,7cm,15cm
C. 13cm,12cm,20cm D. 5cm,5cm,11cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一元二次方程x2-2x+1=0 的根的情況為( )
A. 有兩個相等的實數根 B. 有兩個不相等的實數根
C. 只有一個實數根 D. 沒有實數根
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com