【題目】如圖，四邊形ABCD是平行四邊形，E、F是對角線AC上的兩點，∠1=∠2．
（1）求證：AE=CF；
（2）求證：四邊形EBFD是平行四邊形．
【答案】（1）證明見解析；（2）證明見解析.
【解析】（1）通過證明△ADE≌△CBF，由全等三角的對應邊相等證得AE=CF。
（2）根據平行四邊形的判定定理：對邊平行且相等的四邊形是平行四邊形證得結論。
證明：（1）如圖：∵四邊形ABCD是平行四邊形，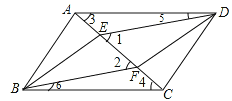
∴AD=BC，AD∥BC，∠3=∠4。
∵∠1=∠3+∠5，∠2=∠4+∠6，
∴∠1=∠2。
∴∠5=∠6。
∵在△ADE與△CBF中，∠3=∠4，AD=BC，∠5=∠6，
∴△ADE≌△CBF（ASA）。
∴AE=CF。
（2）∵∠1=∠2，∴DE∥BF。
又∵由（1）知△ADE≌△CBF，
∴DE=BF。
∴四邊形EBFD是平行四邊形.
“點睛”本題考查了平行四邊形的判定和性質，全等三角形的判定和性質，靈活運用平行四邊形的判定定理是解題關鍵.
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系
中，拋物線
的對稱軸是直線
．
（1）求拋物線的表達式；
（2）點
， 
在拋物線上，若
，請直接寫出
的取值范圍；
（3）設點
為拋物線上的一個動點，當
時，點
關于
軸的對稱點都在直線
的上方，求
的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】根據下列已知條件，能唯一畫出△ABC的是（ ）
A.AB＝6，BC＝3，AC＝9B.AB＝5，BC＝4，∠A＝30°
C.∠C＝90°，AB＝6D.∠A＝60°，∠B＝45°，AB＝4
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在ABCD中，E是BC的中點，連接AE并延長交DC的延長線于點F．
（1）求證：AB=CF；
（2）連接DE，若AD=2AB，求證：DE⊥AF．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在我市舉行的中學生春季田徑運動會上，參加男子跳高的15名運動員的成績如下表所示：
成績（m） | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人數 | 1 | 2 | 4 | 3 | 3 | 2 |
這些運動員跳高成績的中位數和眾數分別是（ ）
A.1.70，1.65
B.1.70，1.70
C.1.65，1.70
D.3，4
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】根據表格估計一元二次方程x2+2x﹣4=0的一個解的范圍在（ ）
x | ﹣1 | 0 | 1 | 2 | 3 |
x2+2x﹣4 | ﹣5 | ﹣4 | ﹣1 | 4 | 11 |
A.﹣1＜x＜0
B.0＜x＜1
C.1＜x＜2
D.2＜x＜3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com