
 接OF,設OD=t.
接OF,設OD=t. ;
;
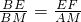 ,即
,即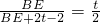 ,
,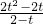 ,
,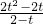 =
= .
. ,
, ;
;
 t=
t= t.
t. =
= t,
t,
 或
或 時,△BEF與△OFE相似.
時,△BEF與△OFE相似. .
.

 名校聯盟快樂課堂系列答案
名校聯盟快樂課堂系列答案科目:初中數學 來源: 題型:
 OAB,C為x軸正半軸上的一個動點(OC>1),連接BC,以BC為邊在第一象限內作等邊△BCD,直線DA交y軸于E點.
OAB,C為x軸正半軸上的一個動點(OC>1),連接BC,以BC為邊在第一象限內作等邊△BCD,直線DA交y軸于E點.查看答案和解析>>
科目:初中數學 來源: 題型:
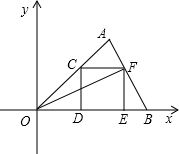
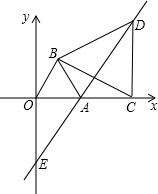
 在直角坐標系中,O為坐標原點,點A的坐標為(2,2),點C是線段OA上的一個動點(不運動至O,A兩點),過點C作CD⊥x軸,垂足為D,以CD為邊在右側作正方形CDEF.連接AF并延長交x軸的正半軸于點B,連接OF,設OD=t.
在直角坐標系中,O為坐標原點,點A的坐標為(2,2),點C是線段OA上的一個動點(不運動至O,A兩點),過點C作CD⊥x軸,垂足為D,以CD為邊在右側作正方形CDEF.連接AF并延長交x軸的正半軸于點B,連接OF,設OD=t.查看答案和解析>>
科目:初中數學 來源: 題型:
| 4 | 3 |
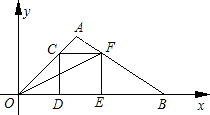
 點B′處,C的對應點為C′.
點B′處,C的對應點為C′.查看答案和解析>>
科目:初中數學 來源: 題型:
| 3 |
| 3 |
| 3 |
| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com