【題目】如圖，在△ABC中，AD是BC邊上的中線，E是AD的中點，過點A作BC的平行線交BE的延長線于點F，連接CF．
（1）求證：AF=DC；
（2）若AB⊥AC，試判斷四邊形ADCF的形狀，并證明你的結論．
【答案】解：（1）證明：∵AF∥BC， ∴∠AFE=∠DBE。
∵E是AD的中點，AD是BC邊上的中線，∴AE=DE，BD=CD。
在△AFE和△DBE中，∵∠AFE=∠DBE，∠FEA=∠BED， AE=DE，
∴△AFE≌△DBE（AAS）。∴AF=BD。
∴AF=DC。
（2）四邊形ADCF是菱形，證明如下：
∵AF∥BC，AF=DC，∴四邊形ADCF是平行四邊形。
∵AC⊥AB，AD是斜邊BC的中線，∴AD=DC。
∴平行四邊形ADCF是菱形
【解析】
試題（1）根據AAS證△AFE≌△DBE，推出AF=BD，即可得出答案。
（2）得出四邊形ADCF是平行四邊形，根據直角三角形斜邊上中線性質得出CD=AD，根據菱形的判定推出即可。
金鑰匙試卷系列答案科目：初中數學 來源： 題型：
【題目】九（3）班為了組隊參加學校舉行的“五水共治”知識競賽，在班里選取了若干名學生，分成人數相同的甲、乙兩組，進行了四次“五水共治”模擬競賽，成績優秀的人數和優秀率分別繪制成如圖統計圖．
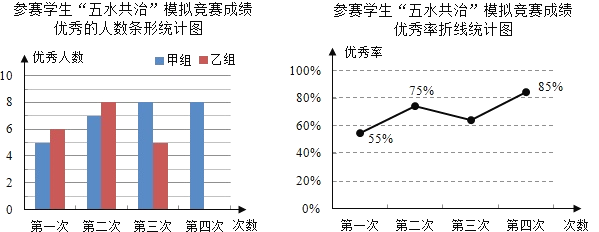
根據統計圖，解答下列問題：
（1）第三次成績的優秀率是多少？并將條形統計圖補充完整；
（2）已求得甲組成績優秀人數的平均數
，方差
，請通過計算說明那一組成績優秀的人數較穩定？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，在四邊形ABCD中，點E、F分別是AB、CD的中點，過點E作AB的垂線，過點F作CD的垂線，兩垂線交于點G，連接AG、BG、CG、DG，且∠AGD=∠BGC．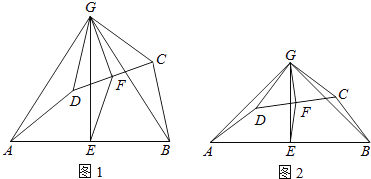
（1）求證：AD=BC；
（2）求證：△AGD∽△EGF；
（3）如圖2，若AD、BC所在直線互相垂直，求 
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△ABC中，點D是邊BC上的點（與B，C兩點不重合），過點D作DE∥AC，DF∥AB，分別交AB，AC于E，F兩點，下列說法正確的是（ ）
A. 若AD⊥BC，則四邊形AEDF是矩形
B. 若AD垂直平分BC，則四邊形AEDF是矩形
C. 若BD=CD，則四邊形AEDF是菱形
D. 若AD平分∠BAC，則四邊形AEDF是菱形
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD所在的網格圖中，每個小正方形的邊長均為1個單位長度．
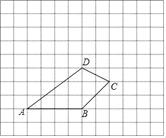
(1)請畫出將四邊形ABCD向上平移5個單位長度，再向左平移2個單位長度后所得的四邊形A′B′C′D′．
(2)求線段AB掃過的面積。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某學校在暑假期間開展“心懷感恩，孝敬父母”的實踐活動，倡導學生在假期中幫助父母干家務，開學以后，校學生會隨機抽取了部分學生，就暑假“平均每天幫助父母干家務所用時長”進行了調查，以下是根據相關數據繪制的統計圖的部分：
根據上述信息，回答下列問題：
在本次隨機抽取的樣本中，調查的學生人數是 人；
，
；
補全頻數分布直方圖；
如果該校共有學生
人，請你估計“平均每天幫助父母干家務的時長不少于
分鐘”的學生大約有多少人？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】將一副三角板中的兩塊直角三角尺的直角頂點
按如圖所示的方式疊放在一起（其中
，
，
），固定三角板
，另一三角板
的
邊從
邊開始繞點順時針旋轉，設旋轉的角度為
．
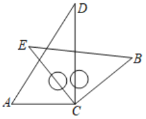
（1）當
時；
①若
，則
的度數為 ；
②若
，求
的度數；
（2）由（1）猜想與的數量關系，并說明理由；
（3）當
時，這兩塊三角尺是否存在一組邊互相垂直？若存在，請直接寫出所有可能的值，并指出哪兩邊互相垂直（不必說明理由）；若不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
