
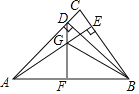
【題目】在△ABC中,∠CAB=45°,BD⊥AC于點D,AE⊥BC于點E,DF⊥AB于點F,AE與DF交于點G,連接BG.
(1)求證:AG=BG;
(2)已知AG=5,BE=4,求AE的長.
科目:初中數學 來源: 題型:
【題目】我們知道,實數與數軸上的點是一一對應的,任意一個實數在數軸上都能找到與之對應的點,比如我們可以在數軸上找到與數字2對應的點.
(1)在如圖所示的數軸上,畫出一個你喜歡的無理數,并用點![]() 表示;
表示;
(2)(1)中所取點![]() 表示的數字是______,相反數是_____,絕對值是______,倒數是_____,其到點5的距離是______.
表示的數字是______,相反數是_____,絕對值是______,倒數是_____,其到點5的距離是______.
(3)取原點為![]() ,表示數字1的點為
,表示數字1的點為![]() ,將(1)中點
,將(1)中點![]() 向左平移2個單位長度,再取其關于點
向左平移2個單位長度,再取其關于點![]() 的對稱點
的對稱點![]() ,求
,求![]() 的長.
的長.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小敏的爸爸買了某項體育比賽的一張門票,她和哥哥兩人都很想去觀看.可門票只有一張,讀九年級的哥哥想了一個辦法,拿了8張撲克牌,將數字為2,3,5,9的四張牌給小敏,將數字為4,6,7,8的四張牌留給自己,并按如下游戲規則進行:小敏和哥哥從各自的四張牌中隨機抽出一張,然后將兩人抽出的兩張撲克牌數字相加,如果和為偶數,則小敏去;如果和為奇數,則哥哥去.
【1】請用畫樹形圖或列表的方法求小敏去看比賽的概率;
【2】哥哥設計的游戲規則公平嗎?若公平,請說明理由;若不公平,請你設計一種公平的游戲規則.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下內容,再解決問題.
在把多項式m2﹣4mn﹣12n2進行因式分解時,雖然它不符合完全平方公式,但是經過變形,可以利用完全平方公式進行分解:
m2﹣4mn﹣12n2=m2﹣4mn+4n2﹣4n2﹣12n2=(m﹣2n)2﹣16n2=(m﹣6n)(m+2n),像這樣構造完全平方式的方法我們稱之為“配方法”,利用這種方法解決下面問題.
(1)把多項式因式分解:a2﹣6ab+5b2;
(2)已知a、b、c為△ABC的三條邊長,且滿足4a2﹣4ab+2b2+3c2﹣4b﹣12c+16=0,試判斷△ABC的形狀.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,定義:在直角三角形ABC中,銳角α的鄰邊與對邊的比叫做角α的余切,記作ctanα,即ctanα=![]() =
=![]() ,根據上述角的余切定義,解下列問題:
,根據上述角的余切定義,解下列問題:
(1)如圖1,若BC=3,AB=5,則ctanB= ;
(2)ctan60°= ;
(3)如圖2,已知:△ABC中,∠B是銳角,ctan C=2,AB=10,BC=20,試求∠B的余弦cosB的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2011年5月20日是第22個中國學生營養日,某校社會實踐小組在這天開展活動,調查快餐營養情況.他們從食品安全監督部門獲取了一份快餐的信息(如圖).根據信息,解答下列問題.
(1)求這份快餐中所含脂肪質量;
(2)若碳水化合物占快餐總質量的40%,求這份快餐所含蛋白質的質量;
(3)若這份快餐中蛋白質和碳水化合物所占百分比的和不高于85%,求其中所含碳水化合物質量的最大值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,AB為⊙O的直徑,C是BA延長線上一點,CP切⊙O于P,弦PD⊥AB于E,過點B作BQ⊥CP于Q,交⊙O于H.
(1)如圖1,求證:PQ=PE;
(2)如圖2,G是圓上一點,∠GAB=30![]() ,連接AG交PD于F,連接BF,tan∠BFE=
,連接AG交PD于F,連接BF,tan∠BFE=![]() ,求∠C的度數;
,求∠C的度數;
(3)如圖3,在(2)的條件下,PD=6![]() ,連接QG交BC于點M,求QM的長.
,連接QG交BC于點M,求QM的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,設二次函數y1=mx2﹣6mx+8m(m為常數).
(1)若函數y1經過點(1,3),求函數y1的表達式;
(2)若m<0,當x<![]() 時,此二次函數y隨x的增大而增大,求a的取值范圍;
時,此二次函數y隨x的增大而增大,求a的取值范圍;
(3)已知一次函數y2=x﹣2,當y1y2>0時,求x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,圖中的小方格都是邊長為1的正方形, △ABC與△A′ B′ C′是關于點0為位似中心的位似圖形,它們的頂點都在小正方形的頂點上.
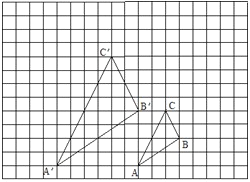
(1)畫出位似中心點0;
(2)求出△ABC與△A′B′C′的位似比;
(3)以點0為位似中心,再畫一個△A1B1C1,使它與△ABC的位似比等于1.5.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com