
【題目】如圖1,在正方形ABCD中,點E為AD上一點,FG⊥CE分別交AB、CD于F、G,垂足為O.
(1)求證:CE=FG;
(2)如圖2,連接OB,若AD=3DE,∠OBC=2∠DCE。
求![]() 的值;
的值;
若AD=3,則OE的長為_________(直接寫出結果).


【答案】![]()
【解析】(1)過點B作BM∥FG交CD于M ,構造三角形,證△BCM≌△CDE,可得; CE=BM=FG;(2) 過點B作BM∥FG交CD于M , 連接MO,由(1)證BC=BO,再證MC=MO=MG=ED,又AD=3DE,所以![]() ;(3)由(1)(2)可得DE=OM=1,BO=AD=3,
;(3)由(1)(2)可得DE=OM=1,BO=AD=3,
又BM=CE=![]() ,再根據面積公式得OC=2×
,再根據面積公式得OC=2×![]() .
.
(1)過點B作BM∥FG交CD于M ,
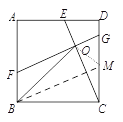
易證四邊形FBMG為平行四邊形
∴FG=BM,
由BC=CD;∠BCM=∠CDE;∠MBC=∠ECD
可證△BCM≌△CDE,
∴CE=BM=FG;
(2)過點B作BM∥FG交CD于M ,
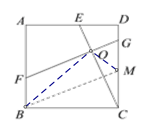
由(1)知△BCM≌△CDE,又∠OBC=2∠DCE ,
MC=ED,∠MBC=∠DCE=∠MBO,
由BM∥FG得MB⊥CE,
∴∠BOC=∠BCO,
∴BC=BO,連接MO,
∴BM垂直平分OC,
∴MC=MO,
又∵∠GOM=∠BMO=∠BMC=∠OGM
∴MC=MO=MG=ED,
又AD=3DE,
∴![]() ;
;
(3)∵AD=3,
∴由(1)(2)可得
DE=OM=1,BO=AD=3,∴BM=CE=![]() ,
,
OC=2×![]() =2×
=2×![]() =
= ![]() ,
, ![]()
![]()
∴OE=CE-CO=![]() .
.


 口算題天天練系列答案
口算題天天練系列答案科目:初中數學 來源: 題型:
【題目】萬州某運輸公司的一艘輪船在長江上航行,往返于萬州、朝天門兩地。假設輪船在靜水中的速度不變,長江的水流速度不變,該輪船從萬州出發,逆水航行到朝天門,停留一段時間(卸貨、裝貨、加燃料等,)又順水航行返回萬州,若該輪船從萬州出發后所用時間為x(小時),輪船距萬州的距離為y(千米),則下列各圖中,能反映y與x之間函數關系的圖象大致是【 】
A. B.
B.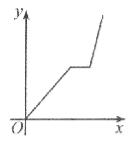 C.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=x2﹣2(m+1)x+m(m+2)
(1)求證:無論m為任何實數,該函數圖象與x軸兩個交點之間的距離為定值.
(2)若該函數圖象的對稱軸為直線x=2,試求二次函數的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點P的坐標為(a,b),點P的“變換點”P`的坐標定義如下:當![]() 時,P`點坐標為(a,-b);當
時,P`點坐標為(a,-b);當![]() 時,P`點坐標為(b,-a)。線段l:
時,P`點坐標為(b,-a)。線段l:![]() 上所有點按上述“變換點”組成一個新的圖形,若直線
上所有點按上述“變換點”組成一個新的圖形,若直線![]() 與組成的新的圖形有兩個交點,則k的取值范圍是( )
與組成的新的圖形有兩個交點,則k的取值范圍是( )
A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
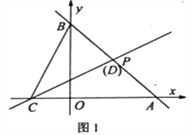
【題目】如圖,直線l1經過過點P(2,2),分別交x軸、y軸于點A(4,0),B。
(1)求直線l1的解析式;
(2)點C為x軸負半軸上一點,過點C的直線l2:![]() 交線段AB于點D。
交線段AB于點D。
如圖1,當點D恰與點P重合時,點Q(t,0)為x軸上一動點,過點Q作QM⊥x軸,分別交直線l1、l2于點M、N。若![]() ,MN=2MQ,求t的值;
,MN=2MQ,求t的值;
如圖2,若BC=CD,試判斷m,n之間的數量關系并說明理由。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】暑假期間,學校組織學生去某景點游玩,甲旅行社說:“如果帶隊的一名老師購買全票,則學生享受半價優惠”; 乙旅行社說:“所有人按全票價的六折優惠”.已知全票價為a元,學生有x人,帶隊老師有1人.
(1)試用含a和x的式子表示甲、乙旅行社的費用;
(2)若有50名學生參加本次活動,請你為他們選擇一家更優惠的旅行社.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,把同樣大小的黑色棋子擺放在正多邊形的邊上,按照這樣的規律擺下去,則第10(n是大于0的整數)個圖形需要黑色棋子的個數是_______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:![]() 、
、![]() 兩地相距
兩地相距![]() ,甲、乙兩車分別從
,甲、乙兩車分別從![]() 、
、![]() 兩地同時出發,甲速每小時
兩地同時出發,甲速每小時![]() 千米,乙速每小時
千米,乙速每小時![]() 千米,請按下列要求列方程解題:
千米,請按下列要求列方程解題:
![]() 若同時出發,相向而行,多少小時相遇?
若同時出發,相向而行,多少小時相遇?
![]() 若同時出發,相向而行,多長時間后兩車相距
若同時出發,相向而行,多長時間后兩車相距![]() ?
?
![]() 若同時出發,同向而行,多長時間后兩車相距
若同時出發,同向而行,多長時間后兩車相距![]() ?
?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com