
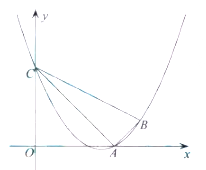
【題目】如圖,已知二次函數![]() 的圖象經過點
的圖象經過點![]() ,
,![]() ,且與
,且與![]() 軸交于點
軸交于點![]() ,連接
,連接![]() 、
、![]() 、
、![]() .
.
(1)求此二次函數的關系式;
(2)判斷![]() 的形狀;若
的形狀;若![]() 的外接圓記為
的外接圓記為![]() ,請直接寫出圓心
,請直接寫出圓心![]() 的坐標;
的坐標;
(3)若將拋物線沿射線![]() 方向平移,平移后點
方向平移,平移后點![]() 、
、![]() 、
、![]() 的對應點分別記為點
的對應點分別記為點![]() 、
、![]() 、
、![]() ,
,![]() 的外接圓記為
的外接圓記為![]() ,是否存在某個位置,使
,是否存在某個位置,使![]() 經過原點?若存在,求出此時拋物線的關系式;若不存在,請說明理由.
經過原點?若存在,求出此時拋物線的關系式;若不存在,請說明理由.
【答案】(1)![]() (2)直角三角形,(2,2)(3)存在,拋物線的關系式為
(2)直角三角形,(2,2)(3)存在,拋物線的關系式為
![]() 或
或![]()
【解析】
試題分析:(1)根據待定系數法可直接代入得到方程組求值,得到函數的解析式;
(2)過點![]() 作
作![]() 軸于點
軸于點![]() ,然后根據角之間的關系得到是直角三角形,最后根據坐標得到D點;
,然后根據角之間的關系得到是直角三角形,最后根據坐標得到D點;
(3)取![]() 中點
中點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,根據勾股定理求出MC的長和OM的長,再通過平移的性質得到平移的距離,然后根據二次函數的平移性質可得到解析式.
,根據勾股定理求出MC的長和OM的長,再通過平移的性質得到平移的距離,然后根據二次函數的平移性質可得到解析式.
試題解析:(1)把點![]() ,
,![]() 代入
代入![]() 中得
中得
![]() ,解得
,解得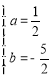 ,
,
所以所求函數的關系式為![]() .
.
(2)![]() 為直角三角形.
為直角三角形.
過點![]() 作
作![]() 軸于點
軸于點![]() ,
,
易知點![]() 坐標為
坐標為![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又因為點![]() 坐標為
坐標為![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() 為直角三角形,
為直角三角形,
圓心![]() 的坐標為
的坐標為![]() .
.
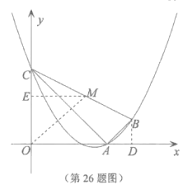
(3)存在.
取![]() 中點
中點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,
,
因為![]() 的坐標為
的坐標為![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,
又因為![]() ,
,
所以![]() ,
,
所以要使拋物線沿射線![]() 方向平移,
方向平移,
且使![]() 經過原點,
經過原點,
則平移的長度為![]() 或
或![]() ,
,
因為![]() ,
,
所以拋物線的頂點向左、向下均分別平移![]() 個單位長度,
個單位長度,
或![]() 個單位長度.
個單位長度.
因為![]() .
.
所以平移后拋物線的關系式為![]() ,
,
即![]()
或![]() ,即
,即![]() .
.
綜上所述,存在一個位置,使![]() 經過原點,此時拋物線的關系式為
經過原點,此時拋物線的關系式為
![]() 或
或![]() .
.


 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:初中數學 來源: 題型:
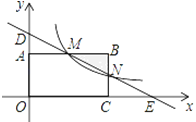
【題目】如圖,在直角坐標系中,矩形OABC的頂點O與坐標原點重合,頂點A,C分別在坐標軸上,頂點B的坐標(4,2),過點D(0,3)和E(6,0)的直線分別于AB,BC交于點M,N.
(1)求直線DE的解析式和點M的坐標;
(2)若反比例函數y=![]() (x>0)的圖象經過點M,求該反比函數的解析式,并通過計算判斷點N是否在該函數的圖象上.
(x>0)的圖象經過點M,求該反比函數的解析式,并通過計算判斷點N是否在該函數的圖象上.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,⊙O的直徑AB=12,P是弦BC上一動點(與點B,C不重合),∠ABC=30°,過點P作PD⊥OP交⊙O于點D.
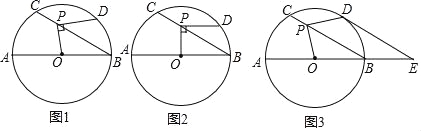
(1)如圖2,當PD∥AB時,求PD的長;
(2)如圖3,當![]() 時,延長AB至點E,使BE=
時,延長AB至點E,使BE=![]() AB,連接DE.
AB,連接DE.
①求證:DE是⊙O的切線;
②求PC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校舉行了“文明在我身邊”攝影比賽.已知每幅參賽作品成績記為![]() 分(
分(![]() ).校方從600幅參賽作品中隨機抽取了部分參賽作品,統計了它們的成績,并繪制了如下不完整的統計圖表.
).校方從600幅參賽作品中隨機抽取了部分參賽作品,統計了它們的成績,并繪制了如下不完整的統計圖表.
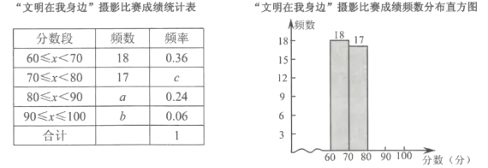
根據以上信息解答下列問題:
(1)統計表中![]() 的值為 ;樣本成績的中位數落在分數段 中;
的值為 ;樣本成績的中位數落在分數段 中;
(2)補全頻數分布直方圖;
(3)若80分以上(含80分)的作品將被組織展評,試估計全校被展評作品數量是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點P(x,y)到x軸的距離為2,到y軸的距離為3,且x+y>0,xy<0,則點P的坐標為( )
A.(﹣2,3)B.(2,3)C.(3,﹣2)D.(3,2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(黃石中考)一食堂需要購買盒子存放食物,盒子有A,B兩種型號,單個盒子的容量和價格如表所示,現有15升食物需要存放且要求每個盒子要裝滿,由于A型號盒子正做促銷互動:購買三個及三個以上可一次性返現金4元,則購買盒子所需要最少費用為_______元.
型號 | A | B |
單個盒子容量(升) | 2 | 3 |
單價(元) | 5 | 6 |
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,10個不同的正偶數按下圖排列,箭頭上方的每個數都等于其下方兩數的和,如![]() ,
,![]() 表示a1=a2+a3,則a1的最小值為( )
表示a1=a2+a3,則a1的最小值為( )

A.32 B.36 C.38 D.40
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com