
【題目】如圖,在△ABC中,∠A=90°,O是BC邊上一點,以O為圓心的半圓分別與AB、AC邊相切于D、E兩點,連接OD.已知BD=2,AD=3. 
求:
(1)tanC;
(2)圖中兩部分陰影面積的和.
【答案】
(1)解:連接OE,
∵AB、AC分別切⊙O于D、E兩點,
∴AD⊥OD,AE⊥OE,
∴∠ADO=∠AEO=90°,
又∵∠A=90°,
∴四邊形ADOE是矩形,
∵OD=OE,
∴四邊形ADOE是正方形,
∴OD∥AC,OD=AD=3,
∴∠BOD=∠C,
∴在Rt△BOD中, ![]() ,
,
∴ ![]() .
.
答:tanC= ![]()
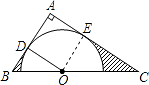
(2)解:如圖,設⊙O與BC交于M、N兩點,
由(1)得:四邊形ADOE是正方形,
∴∠DOE=90°,
∴∠COE+∠BOD=90°,
∵在Rt△EOC中, ![]() =
= ![]() ,OE=3,
,OE=3,
∴ ![]() ,
,
∴S扇形DOM+S扇形EON=S扇形DOE= ![]() ,
,
∴S陰影=S△BOD+S△COE﹣(S扇形DOM+S扇形EON)= ![]() ,
,
答:圖中兩部分陰影面積的和為 ![]() .
.

【解析】(1)連接OE,得到∠ADO=∠AEO=90°,根據∠A=90°,推出矩形ADOE,進一步推出正方形ADOE,得出OD∥AC,OD=AD=3,∠BOD=∠C,即可求出答案;(2)設⊙O與BC交于M、N兩點,由(1)得:四邊形ADOE是正方形,推出∠COE+∠BOD=90°,根據 ![]() ,OE=3,求出
,OE=3,求出 ![]() ,根據S扇形DOM+S扇形EON=S扇形DOE , 即可求出陰影部分的面積.
,根據S扇形DOM+S扇形EON=S扇形DOE , 即可求出陰影部分的面積.


科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點C是⊙O上一點,連接BC,AC,OD⊥BC于E. 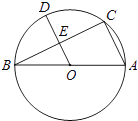
(1)求證:OD∥AC;
(2)若BC=8,DE=3,求⊙O的直徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 
(1)如圖,AB⊥BD于點B,ED⊥BD于點D,AE交BD于點C,且BC=DC.求證:AB=ED.
(2)植樹節期間,兩所學校共植樹834棵,其中海石中學植樹的數量比勵東中學的2倍少3棵,兩校各植樹多少棵?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知點A(0,2),△AOB為等邊三角形,P是x軸上一個動點(不與原O重合),以線段AP為一邊在其右側作等邊三角形△APQ.

(1)求點B的坐標;
(2)在點P的運動過程中,∠ABQ的大小是否發生改變?如不改變,求出其大小;如改變,請說明理由.
(3)連接OQ,當OQ∥AB時,求P點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 市、
市、![]() 市和
市和![]() 市分別有某種機器
市分別有某種機器![]() 臺、
臺、![]() 臺、
臺、![]() 臺,現在決定把這些機器支援給
臺,現在決定把這些機器支援給![]() 市
市![]() 臺,
臺,![]() 市
市![]() 臺.己知調運機器的費用如表所示.
臺.己知調運機器的費用如表所示.
|
|
| |
|
|
|
|
|
|
|
|
設從![]() 市、
市、![]() 市各調
市各調![]() 臺到
臺到![]() 市.
市.
(1)![]() 市調運到
市調運到![]() 市的機器為________臺 (用含
市的機器為________臺 (用含![]() 的式子表示);
的式子表示);
(2)![]() 市調運到
市調運到![]() 市的機器的費用為________元(用含
市的機器的費用為________元(用含![]() 的式子表示,并化簡);
的式子表示,并化簡);
(3)求調運完畢后的總運費(用![]() 的式子表示,并化簡);
的式子表示,并化簡);
(4)當![]() 和
和![]() 時,哪種調運方式總運費少?少多少?
時,哪種調運方式總運費少?少多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市計劃在“十周年”慶典當天開展購物抽獎活動,凡當天在該超市購物的顧客,均有一次抽獎的機會,抽獎規則如下:將如圖所示的圓形轉盤平均分成四個扇形,分別標上1,2,3,4四個數字,抽獎者連續轉動轉盤兩次,當每次轉盤停止后指針所指扇形內的數為每次所得的數(若指針指在分界線時重轉);當兩次所得數字之和為8時,返現金20元;當兩次所得數字之和為7時,返現金15元;當兩次所得數字之和為6時返現金10元. 
(1)試用樹狀圖或列表的方法表示出一次抽獎所有可能出現的結果;
(2)某顧客參加一次抽獎,能獲得返還現金的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“校園安全”受到全社會的廣泛關注,信豐縣某中學對部分學生就校園安全知識的了解程度,采用隨機抽樣調查的方式,并根據收集到的信息進行統計,繪制了如圖所示的兩幅尚不完整的統計圖.請你根據統計圖中所提供的信息解答下列問題
(1)接受問卷調查的學生共有 人,扇形統計圖中“基本了解”部分所對應扇形圓心角是 度;
(2)請補全條形統計圖;
(3)若該中學共有學生1200人,請根據上述調查結果,估計該中學學生中對校園安全知識達到“了解”和“基本了解”程度的總人數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=6cm,AC=8cm,BC=10cm,M是BC邊上的動點,MD⊥AB,ME⊥AC,垂足分別是D、E,線段DE的最小值是 cm.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com