
【題目】有兩個內角分別是它們對角的一半的四邊形叫做半對角四邊形.
(1)如圖1,在半對角四邊形ABCD中,∠B= ![]() ∠D,∠C=
∠D,∠C= ![]() ∠A,求∠B與∠C的度數之和;
∠A,求∠B與∠C的度數之和;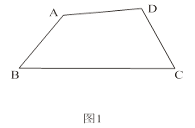
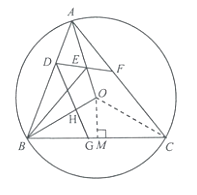
(2)如圖2,銳角△ABC內接于⊙O,若邊AB上存在一點D,使得BD=BO.∠OBA的平分線交OA于點E,連結DE并延長交AC于點F,∠AFE=2∠EAF.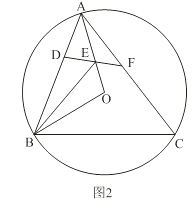
求證:四邊形DBCF是半對角四邊形;
(3)如圖3,在(2)的條件下,過點D作DG⊥OB于點H,交BC于點G.當DH=BG時,求△BGH與△ABC的面積之比.
【答案】
(1)
解:在半對角四邊形ABCD中,∠B=![]() ∠D,∠C=
∠D,∠C=![]() ∠A.
∠A.
∵∠A+∠B+∠C+∠D=360°,
∴3∠B+3∠C=360°.
∴∠B+∠C=120°.
即∠B與∠C的度數之和120°.
(2)
證明:在△BED和△BEO中,
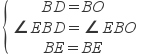 .
.
∴△BED≌△BEO(SAS).
∴∠BDE=∠BOE.
又∵∠BCF=![]() ∠BOE.
∠BOE.
∴∠BCF=![]() ∠BDE.
∠BDE.
如下圖,連結OC.
設∠EAF=![]() .則∠AFE=2∠EAF=2
.則∠AFE=2∠EAF=2![]() .
.
∴∠EFC=180°-∠AFE=180°-2![]() .
.
∵OA=OC,
∴∠OAC=∠OCA=![]() .
.
∴∠AOC=180°-∠OAC-∠OCA=180°-2![]() .
.
∴∠ABC=![]() ∠AOC=
∠AOC=![]() ∠EFC.
∠EFC.
∴四邊形DBCF是半對角四邊形.
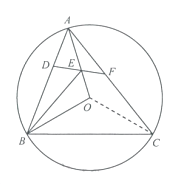
(3)
解:如下圖,作過點OM⊥BC于點M.
∵四邊形DBCF是半對角四邊形,
∴∠ABC+∠ACB=120°.
∴∠BAC=60°.
∴∠BOC=2∠BAC=120°.
∵OB=OC
∴∠OBC=∠OCB=30°.
∴BC=2BM=![]() BO=
BO=![]() BD.
BD.
∵DG⊥OB,
∴∠HGB=∠BAC=60°.
∵∠DBG=∠CBA,
∴△DBG![]() △CBA.
△CBA.
∴![]() =
=![]() 2=
2=![]() .
.
∵DH=BG,BG=2HG.
∴DG=3HG.
∴![]() =
=![]()
∴![]() =
=![]() .
.
【解析】(1)在半對角四邊形ABCD中,∠B=![]() ∠D,∠C=
∠D,∠C=![]() ∠A;根據四邊形的內角和為360°,得出∠B與∠C的度數之和.
∠A;根據四邊形的內角和為360°,得出∠B與∠C的度數之和.
(2)如圖連接OC,根據條件先證△BED≌△BEO,再根據全等三角形的性質得出∠BCF=![]() ∠BOE=
∠BOE=![]() ∠BDE;設∠EAF=
∠BDE;設∠EAF=![]() .則∠AFE=2∠EAF=2
.則∠AFE=2∠EAF=2![]() 得出∠EFC=180°-∠AFE=180°-2
得出∠EFC=180°-∠AFE=180°-2![]() ;再根據OA=OC得出∠OAC=∠OCA=
;再根據OA=OC得出∠OAC=∠OCA=![]() , 根據三角形內角和得出∠AOC=180°-∠OAC-∠OCA=180°-2
, 根據三角形內角和得出∠AOC=180°-∠OAC-∠OCA=180°-2![]() ;從而得證.
;從而得證.
(3)如下圖,作過點OM⊥BC于點M,由四邊形DBCF是半對角四邊形,得出∠ABC+∠ACB=120°,∠BAC=60°.∠BOC=2∠BAC=120°;再由OB=OC,得出∠OBC=∠OCB=30°.BC=2BM=![]() BO=
BO=![]() BD;根據△DBG~△CBA得出答案.
BD;根據△DBG~△CBA得出答案.
【考點精析】掌握三角形的內角和外角和等腰三角形的性質是解答本題的根本,需要知道三角形的三個內角中,只可能有一個內角是直角或鈍角;直角三角形的兩個銳角互余;三角形的一個外角等于和它不相鄰的兩個內角的和;三角形的一個外角大于任何一個和它不相鄰的內角;等腰三角形的兩個底角相等(簡稱:等邊對等角).


科目:初中數學 來源: 題型:
【題目】如圖:
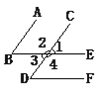
(1)如果∠1=∠B,那么_______∥_______,根據是__________________________;
(2)如果∠3=∠D,那么_______∥_______,根據是__________________________;
(3)如果要使BE∥DF,必須∠1=∠_______,根據是_________________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水果種植場今年收獲的“妃子笑”和“無核Ⅰ號”兩種荔枝共3200 千克,全部售出后賣了30400 元.已知“妃子笑”荔枝每千克售價8 元,“無核Ⅰ號”荔枝每千克售價12 元,問該種植場今年這兩種荔枝各收獲多少千克?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正比例函數 ![]() 的圖象與反比例函數
的圖象與反比例函數 ![]() 的圖象交于A、B兩點,點C在x軸負半軸上,AC=AO,△ACO的面積為12.
的圖象交于A、B兩點,點C在x軸負半軸上,AC=AO,△ACO的面積為12.
(1)求k的值;
(2)根據圖象,當 ![]() 時,寫出自變量
時,寫出自變量 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為積極響應南充市創建“全國衛生城市”的號召,某校1 500名學生參加了衛生知識競賽,成績記為A、B、C、D四等。從中隨機抽取了部分學生成績進行統計,繪制成如下兩幅不完整的統計圖表,根據圖表信息,以下說法不正確的是( )

A.樣本容量是200
B.D等所在扇形的圓心角為15°
C.樣本中C等所占百分比是10%
D.估計全校學生成績為A等大約有900人
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某長途汽車客運公司規定旅客可免費攜帶一定質量的行李,當行李的質量超過規定時,需付的行李費 ![]() (元)是行李質量
(元)是行李質量 ![]() (
( ![]() )的一次函數.已知行李質量為
)的一次函數.已知行李質量為 ![]()
![]() 時需付行李費
時需付行李費 ![]() 元,行李質量為
元,行李質量為 ![]()
![]() 時需付行李費
時需付行李費 ![]() 元.
元.
(1)當行李的質量 ![]() 超過規定時,求
超過規定時,求 ![]() 與
與 ![]() 之間的函數表達式;
之間的函數表達式;
(2)求旅客最多可免費攜帶行李的質量.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,O為直線AB上一點,∠AOC=50°,OD平分∠AOC,∠DOE=90°,
(1)求∠BOC的度數;
(2)通過計算判斷OE是否平分∠BOC.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
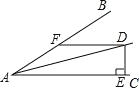
【題目】如圖∠BAC=30°,D 為角平分線上一點,DE⊥AC 于 E,DF∥AC且交AB于F.
(1)求證:△ADF 是等腰三角形.
(2)若 DF=10cm,求 DE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com