
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 為直徑的
為直徑的![]() 交
交![]() 于點
于點![]() ,連結
,連結![]() ,過點
,過點![]() 作
作![]() 交
交![]() 點
點![]() .連接
.連接![]() 交
交![]() 于點
于點![]() .
.
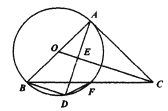
(1)求證:![]() .
.
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)證明見解析;(2)![]()
【解析】
(1)由AAS證明![]() 即可解答;(2)證明OE是△ABD的中位線,可得BD=2OE=2,(1)中全等得AE=BD=2,由勾股定理得
即可解答;(2)證明OE是△ABD的中位線,可得BD=2OE=2,(1)中全等得AE=BD=2,由勾股定理得![]() ,
,![]() ,又因為Rt△ABC是等腰直角三角形,BC=2
,又因為Rt△ABC是等腰直角三角形,BC=2![]() ,由三線合一得BF=FC=
,由三線合一得BF=FC=![]() BC=
BC=![]() ,因為在
,因為在![]() 中,
中,![]() ,所以設
,所以設![]() ,則
,則![]() ,
,![]() ,在Rt△BDH中,由勾股定理得:
,在Rt△BDH中,由勾股定理得:![]() ,解得
,解得![]() ,
,![]() (舍),再由勾股定理得
(舍),再由勾股定理得![]() .
.
(1)∵![]() 為直徑,∴
為直徑,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]()
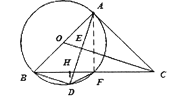
(2)連結![]() ,作
,作![]() ,則
,則![]() .
.
∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,AD=4.
,AD=4.
∴![]() ,
,![]() ,AC=
,AC=![]() ,
,
∵Rt△ABC是等腰直角三角形,BC=2![]() ,由三線合一得BF=FC=
,由三線合一得BF=FC=![]() BC=
BC=![]() ,
,
在![]() 中,
中,![]() ,
,
設![]() ,則
,則![]() ,
,![]() ,
,
∴在Rt△BDH中,由勾股定理得:![]() ,解得
,解得![]() ,
,![]() (舍),
(舍),
∴![]() ,(連結
,(連結![]() ,
,![]() ,證
,證![]() ,證等腰直角
,證等腰直角![]() 亦可)
亦可)


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:初中數學 來源: 題型:
【題目】(1)如圖1,在矩形ABCD中,AB=2,BC=5,∠MPN=90°,且∠MPN的直角頂點在BC邊上,BP=1.
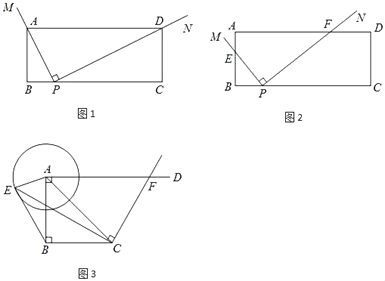
①特殊情形:若MP過點A,NP過點D,則![]() = .
= .
②類比探究:如圖2,將∠MPN繞點P按逆時針方向旋轉,使PM交AB邊于點E,PN交AD邊于點F,當點E與點B重合時,停止旋轉.在旋轉過程中,![]() 的值是否為定值?若是,請求出該定值;若不是,請說明理由.
的值是否為定值?若是,請求出該定值;若不是,請說明理由.
(2)拓展探究:在Rt△ABC中,∠ABC=90°,AB=BC=2,AD⊥AB,⊙A的半徑為1,點E是⊙A上一動點,CF⊥CE交AD于點F.請直接寫出當△AEB為直角三角形時![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
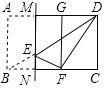
【題目】如圖,在矩形ABCD中,AB:BC=3:5,點E是對角線BD上一動點(不與點B,D重合),將矩形沿過點E的直線MN折疊,使得點A,B的對應點G,F分別在直線AD與BC上,當△DEF為直角三角形時,CN:BN的值為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2014湖南懷化)兩個城鎮(zhèn)A、B與兩條公路ME、MF位置如圖所示,其中ME是東西方向的公路.現電信部門需在C處修建一座信號發(fā)射塔,要求發(fā)射塔到兩個城鎮(zhèn)A、B的距離相等,到兩條公路ME、MF的距離也必須相等,且在∠FME的內部.
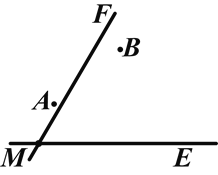
(1)那么點C應選在何處?請在圖中,用尺規(guī)作圖找出符合條件的點C(不寫已知、求作、作法,只保留作圖痕跡);
(2)設AB的垂直平分線交ME于點N,且![]() km,在M處測得點C位于點M的北偏東60°方向,在N處測得點C位于點N的北偏西45°方向,求點C到公路ME的距離.
km,在M處測得點C位于點M的北偏東60°方向,在N處測得點C位于點N的北偏西45°方向,求點C到公路ME的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與
與![]() 軸,
軸,![]() 軸分別交于
軸分別交于![]() ,
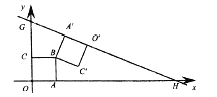
,![]() 兩點,邊長為2的正方形
兩點,邊長為2的正方形![]() 的邊
的邊![]() ,
,![]() 分別在
分別在![]() 軸,
軸,![]() 軸上,點
軸上,點![]() 在第一象限,正方形
在第一象限,正方形![]() 繞點
繞點![]() 逆時針旋轉,
逆時針旋轉,![]() 的對應邊
的對應邊![]() 恰好落在直線
恰好落在直線![]() 上,則
上,則![]() 的值為( )
的值為( )
A. ![]() B.
B. ![]() C. 5D. 6
C. 5D. 6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】發(fā)散思維2017·豐臺區(qū)二模為了解某校八年級學生每周上網的時間,兩名學生進行了抽樣調查,小麗調查了八年級電腦愛好者中40名學生每周上網的時間,小杰從全校400名八年級學生中隨機抽取了40名學生,調查了他們每周上網的時間.小麗與小杰整理各自的樣本數據,如下表所示:
時間段(時/周) | 小麗抽樣人數 | 小杰抽樣人數 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(表中每組數據包含最小值,不包含最大值)
(1)你認為哪名同學抽取的樣本不合理?請說明理由;
(2)專家建議每周上網2小時以上(含2小時)的同學應適當減少上網的時間,估計該校全體八年級學生中有多少名學生應適當減少上網的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
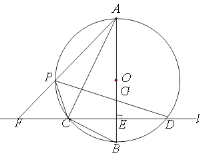
【題目】如圖,在⊙O的內接三角形ABC中,![]() ,
,![]() ,過C作AB的垂線l交⊙O于另一點D,垂足為E.設P是
,過C作AB的垂線l交⊙O于另一點D,垂足為E.設P是![]() 上異于A,C的一個動點,射線AP交l于點F,連接PC與PD,PD交AB于點G.
上異于A,C的一個動點,射線AP交l于點F,連接PC與PD,PD交AB于點G.
(1)求證:![]() ;
;
(2)若![]() ,
, ![]() ,求PD的長.
,求PD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商品的進價為每件50元.當售價為每件70元時,每星期可賣出300件,現需降價處理,且經市場調查:每降價1元,每星期可多賣出20件.在確保盈利的前提下,解答下列問題:
(1)若設每件降價x元、每星期售出商品的利潤為y元,請寫出y與x的函數關系式,并求出自變量x的取值范圍;
(2)當降價多少元時,每星期的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
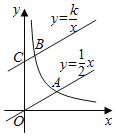
【題目】如圖,直線y=![]() x與雙曲線y=
x與雙曲線y=![]() (k>0,x>0)交于點A,將直線y=
(k>0,x>0)交于點A,將直線y=![]() x向上平移2個單位長度后,與y軸交于點C,與雙曲線交于點B,若OA=3BC,則k的值為____.
x向上平移2個單位長度后,與y軸交于點C,與雙曲線交于點B,若OA=3BC,則k的值為____.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com