
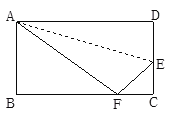
【題目】如圖,小瑩用一張長方形紙片ABCD進行折紙,已知該紙片寬AB為8cm,BC長為10cm.當小瑩折疊時,頂點D落在BC邊上的點F處(折痕為AE).則此時EC=( )cm
A.4B.![]() C.
C.![]() D.3
D.3
【答案】D
【解析】
根據矩形的性質得AB=CD=8,BC=AD=10,∠B=∠C=90°,再根據折疊的性質得AF=AD=10,DE=EF,在Rt△ABF中,利用勾股定理計算出BF=6,則CF=BC﹣BF=4,設CE=x,則DE=EF=8﹣x,在Rt△CEF中利用勾股定理得到:42+x2=(8﹣x)2,然后解方程即可.
解:∵四邊形ABCD為矩形,∴AB=CD=8,BC=AD=10,∠B=∠C=90°.
∵長方形紙片ABCD折紙,頂點D落在BC邊上的點F處(折痕為AE),
∴AF=AD=10,DE=EF,
在Rt△ABF中,AB=8,AF=10,∴BF=![]()
∴CF=BC﹣BF=4.
設CE=x,則DE=EF=8﹣x,
在Rt△CEF中,∵CF2+CE2=EF2,
∴42+x2=(8﹣x)2,解得x=3
∴EC的長為3cm.
故選:D


科目:初中數學 來源: 題型:
【題目】(2015桂林)“全民閱讀”深入人心,好讀書,讀好書,讓人終身受益.為滿足同學們的讀書需求,學校圖書館準備到新華書店采購文學名著和動漫書兩類圖書.經了解,20本文學名著和40本動漫書共需1520元,20本文學名著比20本動漫書多440元(注:所采購的文學名著價格都一樣,所采購的動漫書價格都一樣).
(1)求每本文學名著和動漫書各多少元?
(2)若學校要求購買動漫書比文學名著多20本,動漫書和文學名著總數不低于72本,總費用不超過2000元,請求出所有符合條件的購書方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】勾股定理是幾何中的一個重要定理.在我國古算書《周髀算經》中就有“若勾三,股四,則弦五”的記載.如圖1是由邊長相等的小正方形和直角三角形構成的,可以用其面積關系驗證勾股定理.圖2是把圖1放入長方形內得到的,![]() ,AB=3,AC=4,點D,E,F,G,H,I都在長方形KLMJ的邊上,則長方形KLMJ的面積為___.
,AB=3,AC=4,點D,E,F,G,H,I都在長方形KLMJ的邊上,則長方形KLMJ的面積為___.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線y=x-6與x軸、y軸分別交于點A、B,點E從B點,出發以每秒1個單位的速度沿線段BO向O點移動(與B、O點不重合),過E作EF//AB,交x軸于F.將四邊形ABEF沿EF折疊,得到四邊形DCEF,設點E的運動時間為t秒.
(1)①直線y=x-6與坐標軸交點坐標是A(_____,______),B(______,_____);
②畫出t=2時,四邊形ABEF沿EF折疊后的圖形(不寫畫法);
(2)若CD交y軸于H點,求證:四邊形DHEF為平行四邊形;并求t為何值時,四邊形DHEF為菱形(計算結果不需化簡);
(3)連接AD,BC四邊形ABCD是什么圖形,并求t為何值時,四邊形ABCD的面積為36?

查看答案和解析>>
科目:初中數學 來源: 題型:
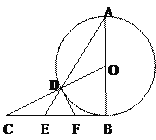
【題目】如圖:已知AB是⊙O的直徑,BC是⊙O的切線,OC與⊙O相交于點D,連結AD并延長,與BC相交于點E。
(1)若BC=![]() ,CD=1,求⊙O的半徑;
,CD=1,求⊙O的半徑;
(2)取BE的中點F,連結DF,求證:DF是⊙O的切線。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小紅同學要測量![]() ,
,![]() 兩地的距離,但
兩地的距離,但![]() ,
,![]() 之間有一水池,不能直接測量,于是她在
之間有一水池,不能直接測量,于是她在![]() ,
,![]() 同一水平面上選取了一點
同一水平面上選取了一點![]() ,點
,點![]() 可直接到達
可直接到達![]() ,
,![]() 兩地.她測量得到
兩地.她測量得到![]() 米,
米,![]() 米,
米,![]() .請你幫助小紅同學求出
.請你幫助小紅同學求出![]() ,
,![]() 兩點之間的距離.
兩點之間的距離.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司生產![]() 兩種設備,已知每臺
兩種設備,已知每臺![]() 種設備的成本是
種設備的成本是![]() 種設備的1.5倍,公司若投入6萬元生產
種設備的1.5倍,公司若投入6萬元生產![]() 種設備,投人15萬元生產
種設備,投人15萬元生產![]() 種設備,則可生產兩種設備共40臺.請解答下列問題:
種設備,則可生產兩種設備共40臺.請解答下列問題:
(1)![]() 兩種設備每臺的成本分別是多少萬元?
兩種設備每臺的成本分別是多少萬元?
(2)若![]() 兩種設備每臺的售價分別是5000元、9000元,公司決定生產兩種設備共50臺,且其中
兩種設備每臺的售價分別是5000元、9000元,公司決定生產兩種設備共50臺,且其中![]() 種設備至少生產10臺,計劃銷售后獲利不低于12萬元,請問采用哪種生產方案公司所獲利潤最大?并求出最大利潤.
種設備至少生產10臺,計劃銷售后獲利不低于12萬元,請問采用哪種生產方案公司所獲利潤最大?并求出最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com