
【題目】如圖,在△ABC中,∠B=∠C,∠BAD=34°,且∠ADE=∠AED,則∠CDE=度. 
【答案】17
【解析】解:由三角形的外角性質得,∠ADC=∠B+∠BAD, ∠AED=∠C+∠CDE,
所以,∠ADE=∠ADC﹣∠CDE=∠B+∠BAD﹣∠CDE,
∵∠ADE=∠AED,
∴∠B+∠BAD﹣∠CDE=∠C+∠CDE,
∵∠B=∠C,
∴∠CDE= ![]() ∠BAD,
∠BAD,
∵∠BAD=34°,
∴∠CDE= ![]() ×34°=17°.
×34°=17°.
所以答案是:17°.
【考點精析】掌握三角形的內角和外角和三角形的外角是解答本題的根本,需要知道三角形的三個內角中,只可能有一個內角是直角或鈍角;直角三角形的兩個銳角互余;三角形的一個外角等于和它不相鄰的兩個內角的和;三角形的一個外角大于任何一個和它不相鄰的內角;三角形一邊與另一邊的延長線組成的角,叫三角形的外角;三角形的一個外角等于和它不相鄰的兩個內角的和;三角形的一個外角大于任何一個和它不相鄰的內角.


科目:初中數學 來源: 題型:
【題目】某商店購買60件A商品和30件B商品共用了1080元,購買50件A商品和20件B商品共用了880元.
(1)A、B兩種商品的單價分別是多少元?
(2)已知該商店購買B商品的件數比購買A商品的件數的2倍少4件,如果需要購買A、B兩種商品的總件數不少于32件,且該商店購買的A、B兩種商品的總費用不超過296元,那么該商店有哪幾種購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD.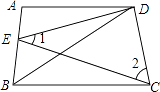
(1)求證:∠1+∠2=90°;
(2)若∠ABD的平分線與CD的延長線交于F,且∠F=55°,求∠ABC;
(3)若H是BC上一動點,F是BA延長線上一點,FH交BD于M,FG平分∠BFH,交DE于N,交BC于G.當H在BC上運動時(不與B點重合), ![]() 的值是否變化?如果變化,說明理由;如果不變,試求出其值.
的值是否變化?如果變化,說明理由;如果不變,試求出其值.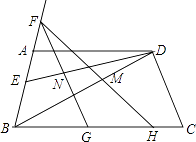
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據等式和不等式的性質,可以得到:若a﹣b>0,則a>b;若a﹣b=0,則a=b;若a﹣b<0,則a<b.這是利用“作差法”比較兩個數或兩個代數式值的大小.
(1)試比較代數式5m2﹣4m+2與4m2﹣4m﹣7的值之間的大小關系;
解:(5m2﹣4m+2)﹣(4m2﹣4m﹣7)=5m2﹣4m+2﹣4m2+4m+7=m2+9,因為m2≥0
所以m2+9>0
所以5m2﹣4m+24m2﹣4m﹣7.(用“>”或“<”填空)
(2)已知A=5m2﹣4( ![]() m﹣
m﹣ ![]() ),B=7(m2﹣m)+3,請你運用前面介紹的方法比較代數式A與B的大小.
),B=7(m2﹣m)+3,請你運用前面介紹的方法比較代數式A與B的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列等式不成立的是( )
A. m2﹣16=(m﹣4)(m+4) B. m2+4m=m(m+4)
C. m2﹣8m+16=(m﹣4)2 D. m2+3m+9=(m+3)2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com