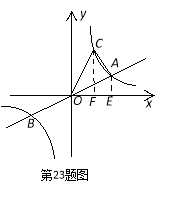
【題目】如圖，已知直線
與雙曲線
交于A、B兩點，點B的坐標為(-4，-2)，C為第一象限內雙曲線
上一點，且點C在直線的上方．
(1)求雙曲線的函數解析式；(2)若△AOC的面積為6，求點C的坐標．
【答案】（1）
（2）（2，4）
【解析】
試題分析：（1）把點B的坐標代入反比例函數解析式求出k值，
（2）再根據反比例函數圖象的中心對稱性求出點A的坐標，然后過點A作AE⊥x軸于E，過點C作CF⊥x軸于F，設點C的坐標為（a， 
），然后根據
列出方程求解即可得到a的值，從而得解．
試題解析：(1)∵點B（﹣4，﹣2）在雙曲線
上，
∴
，∴k=8，
∴雙曲線的函數解析式為
（2）過點A作AE⊥x軸于E，過點C作CF⊥x軸于F，
∵正比例函數與反比例函數的交點A、B關于原點對稱，
∴A（4，2），∴OE＝4，AE＝2，
設點C的坐標為（
，
），則OF＝，CF＝，
則
∵△AOC的面積為6，∴
，
整理得，
，
解得
，
（舍去），
∴點C的坐標為（2，4）．
習題精選系列答案科目：初中數學 來源： 題型：
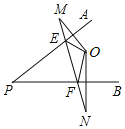
【題目】如圖，已知點O是∠APB內的一點，M，N分別是點O關于PA、PB的對稱點，連接MN，與PA、PB分別相交于點E、F，已知MN=6cm．
（1）求△OEF的周長；
（2）連接PM、PN，若∠APB=ɑ，求∠MPN（用含ɑ的代數式表示）；
（3）當∠ɑ=30°，判定△PMN的形狀，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】上海世博會會期為2010年5月1日至2010年10月31日。門票設個人票和團隊票兩大類。個人普通票160元/張，學生優惠票100元/張；成人團隊票120元/張，學生團隊票50元/張。
（1）如果2名老師、10名學生均購買個人票去參觀世博會，請問一共要花多少元錢購買門票？
（2）用方程組解決下列問題：如果某校共30名師生去參觀世博會，并得知他們都是以團隊形式購買門票，累計花去2200元，請問該校本次分別有多少名老師、多少名學生參觀世博會？
查看答案和解析>>
科目：初中數學 來源： 題型：
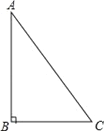
【題目】已知Rt△ABC中，∠B=90°，
（1）根據要求作圖（尺規作圖，保留作圖痕跡，不寫畫法）：
①作∠BAC的平分線AD交BC于D；
②作線段AD的垂直平分線交AB于E，交AC于F，垂足為H；
③連接ED．
（2）在（1）的基礎上寫出一對全等三角形：△ ≌△ 并加以證明．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
