Question

【題目】我們把兩條中線互相垂直的三角形稱為“稱為中垂三角形”，例如圖1，圖2，圖3中，AF，BE是△ABC的中線，AF⊥BE，垂足為P，像△ABC這樣的三角形均稱為“中垂三角形”，設BC=a，AC=b，AB=c．

特例探索

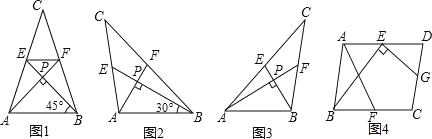
（1）如圖1，當∠ABE=45°，c=2時，a=_____________，b=_____________．

如圖2，當∠ABE=30°，c=4時，a=_____________，b=_____________．

歸納證明

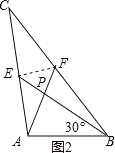
（2）請你觀察（1）中的計算結果，猜想a2，b2，c2三者之間的關系，用等式表示出來，并利用圖3證明你發現的關系式．

拓展應用

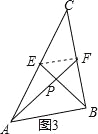
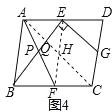
（3）如圖4，在ABCD中，點E、F、G分別是AD，BC，CD的中點，BE⊥EG，AD=2，AB=3，求AF的長．

Answer 1

【答案】（1）2，2，2，2；（2）猜想：a2+b2=5c2，證明見解析；（3）4．

【解析】

試題分析：（1）∵AF⊥BE，∠ABE=45°，∴AP=BP=AB=2，∵AF，BE是△ABC的中線，∴EF∥AB，EF=AB=，∴∠PFE=∠PEF=45°，∴PE=PF=1，在Rt△FPB和Rt△PEA中，AE=BF==，∴AC=BC=2，∴a=b=2，如圖2，連接EF，同理可得：EF=×4=2，∵EF∥AB，∴△PEF～△ABP，∴，在Rt△ABP中，AB=4，∠ABP=30°，∴AP=2，PB=2，∴PF=1，PE=，在Rt△APE和Rt△BPF中，AE=，BF=，∴a=2，b=2，故答案為：2，2，2，2；

（2）猜想：a2+b2=5c2，如圖3，連接EF，設∠ABP=α，∴AP=csinα，PB=ccosα，由（1）同理可得，PF=PA=，PE==，AE2=AP2+PE2=c2sin2α+，BF2=PB2+PF2=+c2cos2α，∴=c2sin2α+， =+c2cos2α，∴+=+c2cos2α+c2sin2α+，∴a2+b2=5c2；

（3）如圖4，連接AC，EF交于H，AC與BE交于點Q，設BE與AF的交點為P，∵點E、G分別是AD，CD的中點，∴EG∥AC，∵BE⊥EG，∴BE⊥AC，∵四邊形ABCD是平行四邊形，∴AD∥BC，AD=BC=2，∴∠EAH=∠FCH，∵E，F分別是AD，BC的中點，∴AE=AD，BF=BC，∴AE=BF=CF=AD=，∵AE∥BF，∴四邊形ABFE是平行四邊形，∴EF=AB=3，AP=PF，在△AEH和△CFH中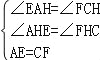，，∴△AEH≌△CFH，∴EH=FH，∴EQ，AH分別是△AFE的中線，由（2）的結論得：AF2+EF2=5AE2，∴AF2=5﹣EF2=16，∴AF=4．