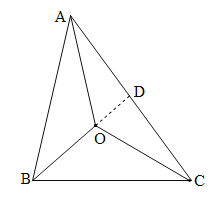
【題目】已知點O在
內部，連接OA，OB，OC，說明：
．
【答案】證明見解析
【解析】
延長BO交AC于D．在△AOB、△BOC、△AOC中，由三角形三邊關系定理列式，三式相加可得2(OA+OB+OC)＞AB+BC+AC，即可證明不等式左邊部分成立．在△ADO、△BDC中，由三角形三邊關系定理列式，兩式相加可得OA+BO＜AC+BC，同理可得：OC+OB＜AB+AC，OC+OA＜AB+BC，三式相加即可證明不等式右邊部分成立．
延長BO交AC于D．
在
中，
，①
在
中
，②
在
中，
，③
①＋②＋③得
．
即
．
在△ADO中，OA＜AD+OD，
在△BDC中，BD＜DC+BC，
∴OA+BD＜AD+OD+DC+BC，
即OA+BO+OD＜AC+OD+BC，
∴OA+BO＜AC+BC ④
同理：
⑤
，⑥
④＋⑤＋⑥得
，
即
．
∴
．
名師點撥卷系列答案
英才計劃期末調研系列答案科目：初中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，有一個等腰直角三角形AOB，∠OAB=90°，直角邊AO在x軸上，且AO=1．將Rt△AOB繞原點O順時針旋轉90°得到等腰直角三角形A1OB1，且A1O=2AO，再將Rt△A1OB1繞原點O順時針旋轉90°得到等腰三角形A2OB2，且A2O=2A1O…，依此規律，得到等腰直角三角形A2017OB2017．則點B2017的坐標_______
查看答案和解析>>
科目：初中數學 來源： 題型：
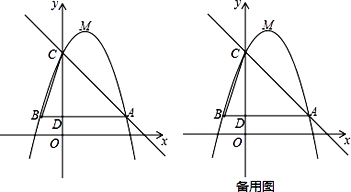
【題目】如圖，已知二次函數y=﹣x2+bx+c（b，c為常數）的圖象經過點A（3，1），點C（0，4），頂點為點M，過點A作AB∥ x軸，交y軸于點D，交該二次函數圖象于點B，連結BC．
(1)求該二次函數的解析式及點M的坐標；
(2)若將該二次函數圖象向下平移m（m＞0）個單位，使平移后得到的二次函數圖象的頂點落在△ ABC的內部（不包括△ ABC的邊界），求m的取值范圍；
(3)點P是直線AC上的動點，若點P，點C，點M所構成的三角形與△ BCD相似，請直接寫出所有點P的坐標（直接寫出結果，不必寫過程）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我國宋朝數學家楊在他的著作《詳解九章算法》中提出“楊輝三角”（如圖所示），此圖揭示了
（n為非負整數）展開式的項數及各項系數的有關規律．
例如：
，它只有一項，系數為1；
，它有兩項，系數分別為1，1，系數和為2；
，它有三項，系數分別為1，2，1，系數和為4；
，它有四項系數分別為1，3，3，1，系數和為8；……根據以上規律，解答下列問題：
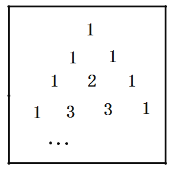
（1）
展開式共有________項，系數分別為________．
（2）展開式共有________項，系數和為________．
（3）
展開結果為________．
（4）利用上面的規律計算：
．
查看答案和解析>>
科目：初中數學 來源： 題型：
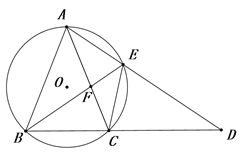
【題目】如圖，△ABC內接于⊙O，且AB＝AC.延長BC到點D，使CD＝CA，連接AD交⊙O于點E.
（1）求證：△ABE≌△CDE；
（2）填空：
①當∠ABC的度數為 時，四邊形AOCE是菱形；
②若AE＝6，BE=8，則EF的長為 .
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某文具商店銷售功能相同的兩種品牌的計算器，購買2個A品牌和1個B品牌的計算器共需122元；購買1個A品牌和2個B品牌的計算器共需124元．
（1）求這兩種品牌計算器的單價；
（2）學校開學前夕，該商店舉行促銷活動，具體辦法如下：購買A品牌計算器按原價的九折銷售，購買B品牌計算器超出10個以上超出的部分按原價的八折銷售，①設購買x個A品牌的計算器需要y1元，購買x個B品牌的計算器需要y2元，分別求出y1、y2關于x的函數關系式；
②小明準備聯系一部分同學集體購買同一品牌的計算器，若購買計算器的數量超過10個，問購買哪種品牌的計算器更合算？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
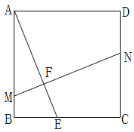
【題目】已知，正方形ABCD中，點E為BC邊上任意一點（點E不與B，C重合），點F在線段AE上，過點F的直線
，分別交AB、CD于點M、N．
（1）如圖，求證：
；
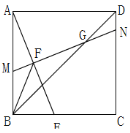
（2）如圖，當點F為AE中點時，連接正方形的對角線BD，MN與BD交于點G，連接BF，求證：
；
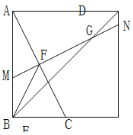
（3）如圖，在（2）的條件下，若
，
，求BM的長度.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點O在直線AB上，OC、OD是兩條射線，OC⊥OD，射線OE平分∠BOC．
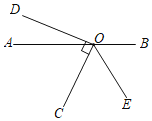
（1）若∠DOE＝150°，求∠AOC的度數．
（2）若∠DOE＝α，則∠AOC＝ ．（請用含α的代數式表示）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
