【題目】如圖，點E、F分別是平行四邊形ABCD的邊BC、AD上的點，且BE＝DF．
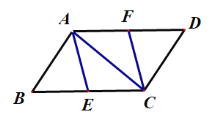
（1）求證：四邊形AECF為平行四邊形；
（2）若AE＝BE，∠BAC＝90°，判斷四邊形AECF的形狀并證明．
【答案】（1）證明見解析；（2）四邊形AECF是菱形.
【解析】
試題（1）通過平行四邊形的判定定理“有一組對邊平行且相等的四邊形是平行四邊形”得出結論：四邊形AECF為平行四邊形；（2）根據R△BAC中角與邊間的關系證得△AEC是等腰三角形，即平行四邊形AECF的鄰邊AE=EC，易證四邊形AECF是菱形．
試題解析：（1）在
ABCD中，AD//BC且AD=BC，
∵BE=DF，∴AF=CE.t
∴AF=CE且AF//CE
∴四邊形AECF是平行四邊形．
（2）四邊形AECF是菱形. 理由如下：
∵AE=BE，∴EAB=EBA
∵BAC=900，∴CBA+BCA=900．
∴EAC=BAC. ∴AE="BE=CE" .
∴四邊形AECF是菱形．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
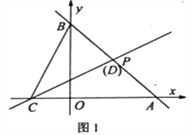
【題目】如圖，直線l1經過過點P（2，2），分別交x軸、y軸于點A（4，0），B。
（1）求直線l1的解析式；
（2）點C為x軸負半軸上一點，過點C的直線l2：
交線段AB于點D。
如圖1，當點D恰與點P重合時，點Q（t，0）為x軸上一動點，過點Q作QM⊥x軸，分別交直線l1、l2于點M、N。若
，MN=2MQ，求t的值；
如圖2，若BC=CD，試判斷m，n之間的數量關系并說明理由。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（閱讀理解）若數軸上兩點A、B所表示的數分別為a和b，則有
①A、B兩點的中點表示的數為
；
②當b＞a時，A、B兩點間的距離為AB＝b﹣a．
（解決問題）數軸上兩點A、B所表示的數分別為a和b，且滿足|a+2|+（b﹣8）2020＝0
（1）求出A、B兩點的中點C表示的數；
（2）點D從原點O點出發向右運動，經過2秒后點D到A點的距離是點D到C點距離的2倍，求點D的運動速度是每秒多少個單位長度？
（數學思考）（3）點E以每秒1個單位的速度從原點O出發向右運動，同時，點M從點A出發以每秒7個單位的速度向左運動，點N從點B出發，以每秒10個單位的速度向右運動，P、Q分別為ME、ON的中點．思考：在運動過程中，
的值是否發生變化？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，矩形紙片ABCD中，G、F分別為AD、BC的中點，將紙片折疊，使D點落在GF上，得到△HAE，再過H點折疊紙片，使B點落在直線AB上，折痕為PQ．連接AF、EF，已知HE=HF，下列結論：①△MEH為等邊三角形；②AE⊥EF；③△PHE∽△HAE；④ 
，其中正確的結論是（ ）
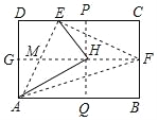
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在《代數式》的學習中,我們通過對同一面積的不同表達和比較,得到合并同類項的法則。下面我們利用這種方法來研究速算。
（1）提出問題：47×43，56×54，89×81，……是一些十位數相同，且個位數之和是10的兩個兩位數相乘的算式，是否可以找到一種速算方法？
（2）幾何建模：
用長方形的面積表示兩個正數的乘積，以47×43為例：
(1)畫長為47，寬為43的矩形，如圖，將這個47×43的矩形從右邊切下長40，寬3的一條，拼接到原長方形上面.
(2)原長方形面積可以有兩種不同的表達方式：47×43的矩形面積或(40+7+3)×40的矩形與右上角3×7的長方形面積之和,即47×43=(40+10)×40+3×7=5×4×100+3×7=2021，
（3）模仿應用:
①請仿照上面的方法使用長方形的面積表示56×54的乘積；
②填空：89×81= ×8×100＋ × =7209;
(4)歸納提煉:
兩個十位數字相同,并且個位數字之和是10的兩位數相乘的速算方法是(用文字表述) .
查看答案和解析>>
科目：初中數學 來源： 題型：
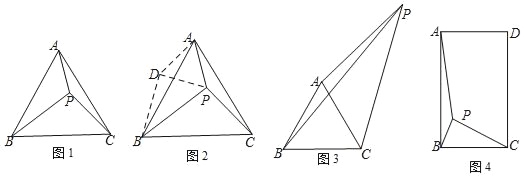
【題目】問題情境：如圖1，在等邊△ABC中，點P在△ABC內，且PA=3，PB=5，PC=4，求∠APC的度數？
小明在解決這個問題時，想到了以下思路：如圖2，把△APC繞著點A順時針旋轉，使點C旋轉到點B，得到△ADB，連結DP．
請你在小明的思路提示下，求出∠APC的度數．
思路應用：如圖3，△ABC為等邊三角形，點P在△ABC外，且PA=6，PC=8，∠APC=30°，求PB的長；
思路拓展：如圖4，矩形ABCD中，AB=
BC，P為矩形ABCD內一點，PA：PB：PC=2
：1：2，則∠APB= °．（直接填空）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，D、E是BC邊上的點，BD：DE：EC=3：2：1，M在AC邊上，CM：MA=1：2，BM交AD，AE于H，G，則BH：HG：GM等于（ ）
A. 4：2：1 B. 5：3：1 C. 25：12：5 D. 51：24：10
查看答案和解析>>
科目：初中數學 來源： 題型：
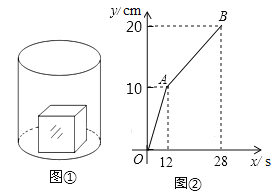
【題目】（2017·吉林）如圖①，一個正方體鐵塊放置在圓柱形水槽內，現以一定的速度往水槽中注水，28s時注滿水槽．水槽內水面的高度y（cm）與注水時間x（s）之間的函數圖象如圖②所示．
（1）正方體的棱長為 cm；
（2）求線段AB對應的函數解析式，并寫出自變量x的取值范圍；
（3）如果將正方體鐵塊取出，又經過t（s）恰好將此水槽注滿，直接寫出t的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
