
【題目】我們把正六邊形對角線的交點稱為它的中心,正六邊形的頂點及它的中心稱作特征點,如圖(1)有六個頂點和一個中心點,因此共有7個特征點,照圖(1)的方式繼續排列正六邊形,使得相鄰兩個正六邊形的一邊重合,這樣得到圖(2),圖(3)…

觀察以上圖形得到表:
圖形的名稱 | 特征點的個數 |
圖1 | 7 |
圖2 | 12 |
… | … |
(1)第n個圖形的特征點有多少個?
(2)第100個圖形的特征點有多少個?
(3)第幾個圖形有2017個特征點?請說明理由.
 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優好卷系列答案
金狀元績優好卷系列答案科目:初中數學 來源: 題型:
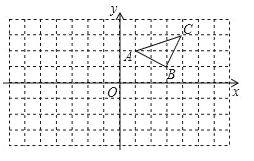
【題目】已知:如圖所示.
(1)作出△ABC關于y軸對稱的△A′B′C′,并寫出△A′B′C′三個頂點的坐標.
(2)在x軸上畫出點P,使PA+PC最小,并直接寫出此時PA+PC的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠接受了20天內生產1200臺GH型電子產品的總任務. 已知每臺GH型產品由4個G型裝置和3個H型裝置配套組成. 工廠現有80名工人,每個工人每天能加工6個G型裝置或3個H型裝置.工廠將所有工人分成兩組同時開始加工,每組分別加工一種裝置,并要求每天加工的G、H型裝置數量正好全部配套組成GH型產品.
(1)按照這樣的生產方式,工廠每天能配套組成多少套GH型電子產品?
(2)為了在規定期限內完成總任務,工廠決定補充一些新工人,這些新工人只能獨立進行G 型裝置的加工,且每人每天只能加工4個G型裝置. 請問至少需要補充多少名新工人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解
∵![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3.
<3.
∴![]() 的整數部分為2,小數部分為
的整數部分為2,小數部分為![]() ﹣2,
﹣2,
∴1<![]() ﹣1<2
﹣1<2
∴![]() ﹣1的整數部分為1.
﹣1的整數部分為1.
∴![]() ﹣1的小數部分為
﹣1的小數部分為![]() ﹣2
﹣2
解決問題:已知:a是![]() ﹣3的整數部分,b是
﹣3的整數部分,b是![]() ﹣3的小數部分,
﹣3的小數部分,
求:(1)a,b的值;
(2)(﹣a)3+(b+4)2的平方根.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列關于自然數的等式:
a1:32-12=8×1;
a2:52-32=8×2;
a3:72-52=8×3;……
根據上述規律解決下列問題:
⑴寫出第a4個等式:___________;
⑵寫出你猜想的第an個等式(用含n的式子表示),并驗證其正確性;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了從甲、乙兩名選手中選拔一人參加射擊比賽,現對他們進行一次測驗,兩個人在相同條件下各射靶10次,為了比較兩人的成績,制作了如下統計圖表:

甲、乙射擊成績統計表
平均數 | 中位數 | 方差 | 命中10環的次數 | |
甲 | 7 | |||
乙 | 1 |
(1)請補全上述圖表(請直接在表中填空和補全折線圖);
(2)如果規定成績較穩定者勝出,你認為誰將勝出?說明你的理由;
(3)如果希望(2)中的另一名選手勝出,根據圖表中的信息,應該制定怎樣的評判規則?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AD∥BC,E為CD的中點,連接AE、BE,BE⊥AE,延長AE交BC的延長線于點F.
求證:(1)FC=AD;
(2)AB=BC+AD.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一張三角形紙片ABC(如圖甲),其中AB=AC.將紙片沿過點B的直線折疊,使點C落到AB邊上的E點處,折痕為BD(如圖乙).再將紙片沿過點E的直線折疊,點A恰好與點D重合,折痕為EF(如圖丙).原三角形紙片ABC中,∠ABC的大小為______°.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,△ABC中,沿∠BAC的平分線AB1折疊,剪掉重疊部分;將余下部分沿∠B1A1C的平分線A1B2折疊,剪掉重疊部分;…;將余下部分沿∠BnAnC的平分線AnBn+1折疊,點Bn與點C重合.無論折疊多少次,只要最后一次恰好重合,我們就稱∠BAC是△ABC的好角.
小麗展示了確定∠BAC是△ABC的好角的兩種情形.情形一:如圖2,沿等腰三角形ABC頂角∠BAC的平分線AB1折疊,點B與點C重合;情形二:如圖3,沿△ABC的∠BAC的平分線AB1折疊,剪掉重疊部分;將余下部分沿∠B1A1C的平分線A1B2折疊,此時點B1與點C重合.
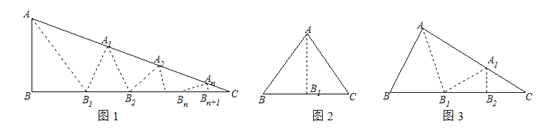
(1)小麗經過三次折疊發現了∠BAC是△ABC的好角,請探究∠B與∠C(不妨設∠B>∠C)之間的等量關系.
(2)根據以上內容猜想:若經過n次折疊∠BAC是△ABC的好角,則∠B與∠C(不妨設∠B>∠C)之間的等量關系為 ;
(3)如果一個三角形的最小角是15°,且滿足該三角形的三個角均是此三角形的好角,則此三角形另兩個角的度數為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com