
【題目】如圖,在平面直角坐標系xOy中,A點的坐標為(1,0).以OA為邊在x軸上方畫一個正方形OABC.以原點O為圓心,正方形的對角線OB長為半徑畫弧,與x軸正半軸交于點D.

(1)點D的坐標是 ;
(2)點P(x,y),其中x,y滿足2x-y=-4.
①若點P在第三象限,且△OPD的面積為3![]() ,求點P的坐標;
,求點P的坐標;
②若點P在第二象限,判斷點E(![]() +1,0)是否在線段OD上,并說明理由.
+1,0)是否在線段OD上,并說明理由.
【答案】(1)(![]() ,0);(2)①P(-5,-6);②點E在線段OD上,見解析.
,0);(2)①P(-5,-6);②點E在線段OD上,見解析.
【解析】
(1)先求出正方形的邊長,再用勾股定理求出OB,即可得出結論;
(2)①先表示出PQ,再利用△ODP的沒解決建立方程求解,即可得出結論;
②根據點P在第二象限,求出x的范圍,進而判斷出點E在x軸正半軸上,即可得出結論.
(1)∵四邊形OABC是正方形,且A(1,0),
∴OA=AB=1,
根據勾股定理得,OB=![]() ,
,
∴OD=![]() ,
,
∴D(![]() ,0),
,0),
故答案為:(![]() ,0);
,0);
(2)①如圖,過點P作PQ⊥x軸于點Q,
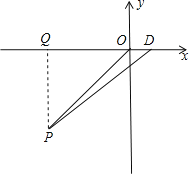
∵點P在第三象限,
∴y=2x+4<0,
∴PQ=-(2x+4),
∵D(![]() ,0),
,0),
∴OD=![]() ,
,
∴S△ODP=![]() ODPQ=3
ODPQ=3![]() ,
,
即:-![]() ×
×![]() ×(2x+4)=3
×(2x+4)=3![]() ,
,
∴x=-5,
∴P(-5,-6);
②點E在線段OD上,
理由:∵2x-y=-4,
∴y=2x+4,
∵點P在第二象限,
∴![]() ,
,
∴-2<x<0,
∴0<![]() x+1<1,
x+1<1,
∴點E在x軸正半軸上,
∵點D在x軸正半軸,OD=![]() ,
,
∴0<OE<OD,
∴點E在線段OD上.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,三角形![]() 是三角形
是三角形![]() 經過某種變換后得到的圖形.
經過某種變換后得到的圖形.

(1)分別寫出點![]() 和點
和點![]() ,點
,點![]() 和點
和點![]() ,點
,點![]() 和點
和點![]() 的坐標;
的坐標;
(2)觀察點![]() 和點
和點![]() ,點
,點![]() 和點
和點![]() ,點
,點![]() 和點
和點![]() 的坐標,用文字語言描述它們的坐標之間的關系______;
的坐標,用文字語言描述它們的坐標之間的關系______;
(3)三角形![]() 內任意一點
內任意一點![]() 的坐標為
的坐標為![]() ,點
,點![]() 經過這種變換后得到點
經過這種變換后得到點![]() ,則點
,則點![]() 的坐標為____.
的坐標為____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小紅和小明在操場做游戲,他們先在地上畫了半徑分別2m和3m的同心圓(如圖),蒙上眼在一定距離外向圈內擲小石子,擲中陰影小紅勝,否則小明勝,未擲入圈內不算,你來當裁判.
(1)你認為游戲公平嗎?為什么?
(2)游戲結束,小明邊走邊想,“反過來,能否用頻率估計概率的方法,來估算某一不規則圖形的面積呢”.請你設計方案,解決這一問題.(要求補充完整圖形,說明設計步驟、原理,寫出估算公式)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(≠0)的圖象如圖,給出下列四個結論:①4ac﹣b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠1),其中結論正確的個數是( )

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,點D是BC邊上的一個動點(不與B、C重合),在AC上取一點E,使∠ADE=30°.
(1)求證:△ABD∽△DCE;
(2)設BD=x,AE=y,求y關于x的函數關系式并寫出自變量x的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國南宋數學家楊輝用三角形解釋二項和的乘方規律,稱之為“楊輝三角”,這個三角形給出了(a+b)n (n=1,2,3,4,…)的展開式的系數規律(按n的次數由大到小的順序):
1 1 (a+b)1=a+b
1 2 1 (a+b)2=a2+2ab+b2
1 3 3 1 (a+b)3=a3+3a2b+3ab2+b3
1 4 6 4 1 (a+b)4=a4+4a3b+6a2b2+4ab3+b4
…… ……
請依據上述規律,寫出(x1)2019展開式中含x2018項的系數是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是邊長為4cm的正方形
是邊長為4cm的正方形![]() 對角線的交點,
對角線的交點,![]() 是
是![]() 的中點,動點
的中點,動點![]() 由點
由點![]() 開始沿折線
開始沿折線![]() 方向勻速運動,到點
方向勻速運動,到點![]() 時停止運動,速度為
時停止運動,速度為![]() .設
.設![]() 點的運動時間為
點的運動時間為![]() ,點
,點![]() 的運動路徑與
的運動路徑與![]() 、
、![]() 所圍成的圖形面積為
所圍成的圖形面積為![]() ,則描述面積
,則描述面積![]() 與時間
與時間![]() 的關系的圖象是( )
的關系的圖象是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠AOB=30°,點P是∠AOB內的定點,且OP=3.若點M、N分別是射線OA、OB上異于點O的動點,則△PMN周長的最小值是( )

A.12B.9C.6D.3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,旗桿AB的頂端B在夕陽的余輝下落在一個斜坡上的點D處,某校數學課外興趣小組的同學正在測量旗桿的高度,在旗桿的底部A處測得點D的仰角為15°,AC=10米,又測得∠BDA=45°.已知斜坡CD的坡度為i=1:![]() ,求旗桿AB的高度(
,求旗桿AB的高度(![]() ≈1.7,結果精確到個位).
≈1.7,結果精確到個位).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com