
【題目】如圖,![]() 的直徑
的直徑![]() 為
為![]() ,弦
,弦![]() 為
為![]() ,
,![]() 、
、![]() 分別是
分別是![]() 的平分線與
的平分線與![]() ,
,![]() 的交點,
的交點,![]() 為
為![]() 延長線上一點,且
延長線上一點,且![]() .
.

![]() 求
求![]() 、
、![]() 的長;
的長;
![]() 試判斷直線
試判斷直線![]() 與
與![]() 的位置關系,并說明理由.
的位置關系,并說明理由.
【答案】(1)![]() ,
,![]() ;
;![]() 直線
直線![]() 與
與![]() 相切,理由詳見解析.
相切,理由詳見解析.
【解析】
(1)連接BD,利用直徑所對的圓周角是直角得兩個直角三角形,再由角平分線得:∠ACD=∠DCB=45°,由同弧所對的圓周角相等可知:△ADB是等腰直角三角形,利用勾股定理可以求出直角邊AD=5![]() ,AC的長也是利用勾股定理列式求得;
,AC的長也是利用勾股定理列式求得;
(2)連接半徑OC,證明垂直即可;利用直角三角形中一直角邊是斜邊的一半得:這條直角邊所對的銳角為30°,依次求得∠COB、∠CEP、∠PCE的度數,最后求得∠OCP=90°,結論得出.
解:(1)連接BD,
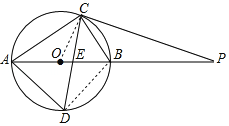
∵AB是⊙O的直徑,
∴∠ACB=∠ADB=90°',
∵CD平分∠ACB,
∴∠ACD=∠DCB=45°,
∴∠ABD=∠ACD=45°,∠DAB=∠DCB=45°,
∴△ADB是等腰直角三角形,
∵AB=10,
∴AD=BD=![]() =5
=5![]() ,
,
在Rt△ACB中,AB=10,BC=5,
∴AC=![]() =5
=5![]() ,
,
∴![]() ,
,![]() ;
;
![]() 直線
直線![]() 與
與![]() 相切,理由是:
相切,理由是:
連接![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴直線![]() 與
與![]() 相切.
相切.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:初中數學 來源: 題型:
【題目】把半徑為![]() 的圓周按
的圓周按![]() 分割為三段.則最短的弧所對的圓心角為________,該弧和半徑圍成的扇形的面積為________,最長的弧所對的圓周角為________,最長的弧長是________.
分割為三段.則最短的弧所對的圓心角為________,該弧和半徑圍成的扇形的面積為________,最長的弧所對的圓周角為________,最長的弧長是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c與x軸交于點A(﹣1,0),頂點坐標是(1,n),與y軸的交點在(0,3)和(0,6)之間(包含端點),則下列結論錯誤的是( )
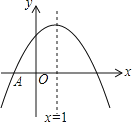
A.3a+b<0B.﹣2≤a≤﹣lC.abc>0D.9a+3b+2c>0
查看答案和解析>>
科目:初中數學 來源: 題型:
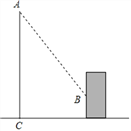
【題目】小左同學想利用影長測量學校旗桿的高度,如圖,她在某一時刻立一長度為1米的標桿,測得其影長為![]() 米,同時旗桿投影的一部分在地上,另一部分在某一建筑物的墻上,測得旗桿與建筑物的距離為10米,旗桿在墻上的影高為2米,請幫小左同學算出學校旗桿的高度.
米,同時旗桿投影的一部分在地上,另一部分在某一建筑物的墻上,測得旗桿與建筑物的距離為10米,旗桿在墻上的影高為2米,請幫小左同學算出學校旗桿的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題8分)如圖,在五邊形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求證:△ABC≌△AED;
(2)當∠B=140°時,求∠BAE的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
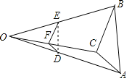
【題目】如圖,己知![]() ,任取一點
,任取一點![]() ,連
,連![]() ,
,![]() ,
,![]() ,并取它們的中點
,并取它們的中點![]() ,
,![]() ,
,![]() ,得
,得![]() ,則下列說法正確的個數是( )
,則下列說法正確的個數是( )
①![]() 與
與![]() 是位似圖形;②
是位似圖形;②![]() 與
與![]() 是相似圖形;
是相似圖形;
③![]() 與
與![]() 的周長比為
的周長比為![]() ;④
;④![]() 與
與![]() 的面積比為
的面積比為![]() .
.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
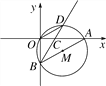
【題目】如圖,在直角坐標系中,⊙M經過原點O(0,0),點A(![]() ,0)與點B(0,-
,0)與點B(0,-![]() ),點D在劣弧
),點D在劣弧![]() 上,連結BD交x軸于點C,且∠COD=∠CBO.
上,連結BD交x軸于點C,且∠COD=∠CBO.
(1)求⊙M的半徑;
(2)求證:BD平分∠ABO;
(3)在線段BD的延長線上找一點E,使得直線AE恰為⊙M的切線,求此時點E的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com