
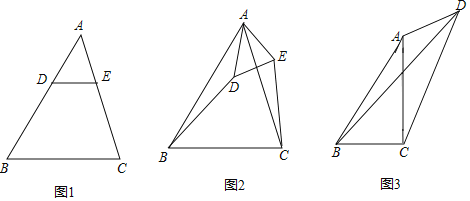
【題目】(1)如圖1,在△ABC中,AB>AC,點D,E分別在邊AB,AC上,且DE∥BC,若AD=2,AE=![]() ,則
,則![]() 的值是 ;
的值是 ;
(2)如圖2,在(1)的條件下,將△ADE繞點A逆時針方向旋轉一定的角度,連接CE和BD,![]() 的值變化嗎?若變化,請說明理由;若不變化,請求出不變的值;
的值變化嗎?若變化,請說明理由;若不變化,請求出不變的值;
(3)如圖3,在四邊形ABCD中,AC⊥BC于點C,∠BAC=∠ADC=θ,且tanθ=![]() ,當CD=6,AD=3時,請直接寫出線段BD的長度.
,當CD=6,AD=3時,請直接寫出線段BD的長度.
【答案】(1)![]() ;(2)
;(2)![]() 的值不變化,值為
的值不變化,值為![]() ,理由見解析;(3)
,理由見解析;(3)![]()
![]()
【解析】
(1)由平行線分線段成比例定理即可得出答案;
(2)證明△ABD∽△ACE,得出![]() =
=![]() =
=![]()
(3)作AE⊥CD于E,DM⊥AC于M,DN⊥BC于N,則DM=CN,DN=MC,由三角函數定義得出![]() =
=![]() ,
,![]() =
=![]() ,得出
,得出![]() =
=![]() ,求出AE=
,求出AE=![]() AD=
AD=![]() ,DE=
,DE=![]() AE=
AE=![]() ,得出CE=CD﹣DE=
,得出CE=CD﹣DE=![]() ,由勾股定理得出AC=
,由勾股定理得出AC=![]() =
=![]() ,得出BC=
,得出BC=![]() AC=
AC=![]()
,由面積法求出CN=DM=![]() ,得出BN=BC+CN=
,得出BN=BC+CN=![]() ,由勾股定理得出AM=
,由勾股定理得出AM=![]() =
=![]() ,得出DN=MC=AM+AC=
,得出DN=MC=AM+AC=![]() ,再由勾股定理即可得出答案.
,再由勾股定理即可得出答案.
(1)∵DE∥BC,
∴![]() =
=![]() =
=![]() =
=![]() ;
;
故答案為:![]() ;
;
(2)![]() 的值不變化,值為
的值不變化,值為![]() ;理由如下:
;理由如下:
由(1)得:DE∥B,
∴△ADE∽△ABC,
∴![]() =
=![]() ,
,
由旋轉的性質得:∠BAD=∠CAE,
∴△ABD∽△ACE,
∴![]() =
=![]() =
=![]() ;
;
(3)作AE⊥CD于E,DM⊥AC于M,DN⊥BC于N,如圖3所示:
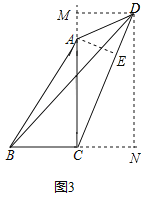
則四邊形DMCN是矩形,
∴DM=CN,DN=MC,
∵∠BAC=∠ADC=θ,且tanθ=![]() ,
,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴AE=![]() AD=
AD=![]() ×3=
×3=![]() ,DE=
,DE=![]() AE=
AE=![]() ,
,
∴CE=CD﹣DE=6﹣![]() =
=![]() ,
,
∴AC=![]() =
=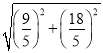 =
=![]()
∴BC=![]() AC=
AC=![]() ,
,
∵△ACD的面積=![]() AC×DM=
AC×DM=![]() CD×AE,
CD×AE,
∴CN=DM=![]() =
=![]() ,
,
∴BN=BC+CN=![]() ,AM=
,AM=![]() =
=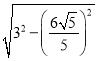 =
=![]() ,
,
∴DN=MC=AM+AC=![]() ,
,
∴BD=![]() =
=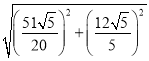 =
=![]()
![]() .
.


 學業測評一課一測系列答案
學業測評一課一測系列答案科目:初中數學 來源: 題型:
【題目】如圖,小明到青城山游玩,乘坐纜車,當登山纜車的吊箱經過點A到達點B時,它經過了200 m,纜車行駛的路線與水平夾角∠α=16°,當纜車繼續由點B到達點D時,它又走過了200 m,纜車由點B到點D的行駛路線與水平夾角∠β=42°,求纜車從點A到點D垂直上升的距離.(結果保留整數)(參考數據:sin16°≈0.27,cos16°≈0.77,sin42°≈0.66,cos42°≈0.74)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有四張背面完全相同的卡片,正面上分別標有數字﹣2,﹣1,1,2.把這四張卡片背面朝上,隨機抽取一張,記下數字為m;放回攪勻,再隨機抽取一張卡片,記下數字為n,則y=mx+n不經過第三象限的概率為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為配合全市“禁止焚燒秸稈”工作,某學校舉行了“禁止焚燒秸稈,保護環境,從我做起”為主題的演講比賽. 賽后組委會整理參賽同學的成績,并制作了如下不完整的頻數分布表和頻數分布直方圖,請根據圖表提供的信息,解答下列問題:
分數段 (分數為x分) | 頻數 | 百分比 |
60≤x<70 | 8 | 20% |
70≤x<80 | a | 30% |
80≤x<90 | 16 | b% |
90≤x<100 | 4 | 10% |
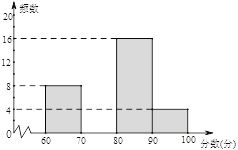
(1)表中的a= ,b= ;
(2)請補全頻數分布直方圖;
(3)若用扇形統計圖來描述成績分布情況,則分數段70≤x<80對應的圓心角的度數是 ;
(4)競賽成績不低于90分的4名同學中正好有2名男同學,2名女同學.學校從這4名同學中隨機抽取2名同學接受電視臺記者采訪,請用列表或畫樹狀圖的方法求正好抽到一名男同學和一名女同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),AB=CD,AD=BC,O為AC中點,過O點的直線分別與AD、BC相交于點M、N,那么∠1與∠2有什么關系?請說明理由;
若過O點的直線旋轉至圖(2)、(3)的情況,其余條件不變,那么圖(1)中的∠1與∠2的關系成立嗎?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學原計劃加工一批校服,現有甲、乙兩個工廠加工這批校服,已知甲工廠每天能加工這種校服16件,乙工廠每天加工這種校服24件,且單獨加工這批校服甲廠比乙廠要多用20天
(1)求這批校服共有多少件?
(2)為了盡快完成這批校服,若先由甲、乙兩工廠按原速度合作一段時間后,甲工廠停工,而乙工廠每天的速度提高25%,乙工廠單獨完成剩下的部分,且乙工廠全部工作時間是甲工廠工作時間的2倍還多4天,求乙工廠加工多少天
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商品現在的售價為每件60元,每星期可賣出300件. 市場調查反映:如調整價格,每降價1元,每星期可多賣出20件. 已知商品的進價為每件40元,如何定價才能使利潤最大?這個最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若該方程有兩個實數根,求m的最小整數值;
(2)若方程的兩個實數根為x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某游客乘坐“金碧皇宮號游船”在長江和嘉陵江的交匯處A點,測得來福土最高樓頂點F的仰角為45°,此時他頭項正上方146米的點B處有架航拍無人機測得來福士最高樓頂點F的仰角為31°,游船朝碼頭方向行駛120米到達碼頭C,沿坡度i=1:2的斜坡CD走到點D,再向前走160米到達來福士樓底E,則來福士最高樓EF的高度約為( )(結果精確到0.1,參考數據:sin31°≈0.52,cos31°≈0.87,tan31°≈0.60)
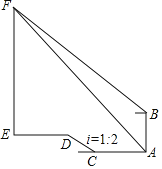
A.301.3米B.322.5米C.350.2米D.418.5米
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com