
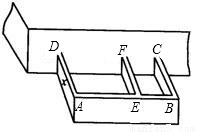
某農戶計劃利用現有的一面墻(墻長8米),再修四面墻,建造如圖所示的長方體水池,培育不同品種的魚苗.他已備足可以修高為1.5m、長18m的墻的材料準備施工,設圖中與現有一面墻垂直的三面墻的長度都為xm,即AD=EF=BC=xm.(不考慮墻的厚度).
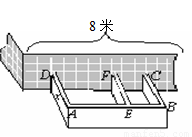
(1)若想水池的總容積為36m3,x應等于多少?
(2)求水池的總容積V與x的函數關系式,并直接寫出x的取值范圍;
(3)若想使水池的總容積V最大,x應為多少?最大容積是多少?
(1)2或4;(2)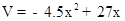 ,x的取值范圍是
,x的取值范圍是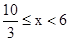 ;(3)當
;(3)當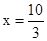 時,總容積V最大=40.
時,總容積V最大=40.
【解析】
試題分析:(1)這個水槽是個長方體,我們先看這個矩形的面積,有了AD、EF、BC的長,因為材料的總長度是18m,因此這個矩形的長應該是18﹣3x,又知道寬為x,又已知了長方體的高,因此可根據長×寬×高=36m3來得出關于x的二次方程從而求出x的值.
(2)和(1)類似,只需把36立方米換成V即可.
(3)此題是求二次函數的最值,可以用配方法或公式法,來求出此時x、y的值.
試題解析:(1)∵AD=EF=BC=x,∴AB=18﹣3x,∴水池的總容積為 ,即
,即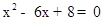 ,解得:x=2或4,所以x應為2m或4m;
,解得:x=2或4,所以x應為2m或4m;
(2)由(1)知V與x的函數關系式為: ,∵AB≤8,∴18-3x≤8,解得x≥
,∵AB≤8,∴18-3x≤8,解得x≥ ,x的取值范圍是:
,x的取值范圍是: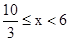 ;
;
(3)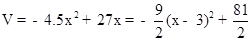 ,∴由函數圖象知:當x=3時,V有最大值40.5.∵
,∴由函數圖象知:當x=3時,V有最大值40.5.∵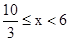 ,∴若使水池的總容積最大,
,∴若使水池的總容積最大,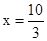 ,最大容積為40m3.
,最大容積為40m3.
考點:1.二次函數的應用;2.應用題.


科目:初中數學 來源: 題型:
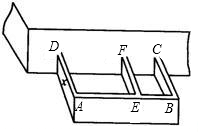 墻垂直的三面墻的長度都為xm,即AD=EF=BC=xm.(不考慮墻的厚度)
墻垂直的三面墻的長度都為xm,即AD=EF=BC=xm.(不考慮墻的厚度)查看答案和解析>>
科目:初中數學 來源:《第26章 二次函數》2010年復習題(解析版) 題型:解答題
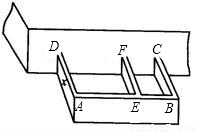
查看答案和解析>>
科目:初中數學 來源:第6章《二次函數》常考題集(18):6.4 二次函數的應用(解析版) 題型:解答題
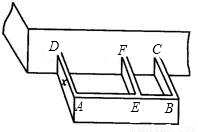
查看答案和解析>>
科目:初中數學 來源:2011年1月浙江省杭州市濱江區九年級(上)月考數學試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com