Question

如圖，下列幾何體是由棱長為1的小立方體按一定規律在地面上擺成的，現將露出的表面都涂上顏色（下底面不涂色），則所給幾何體中只有兩個面涂色的小立方體的個數分別為：

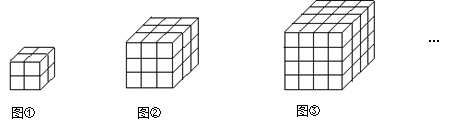
第1個幾何體：最下面一層個數＝4；
第2個幾何體：最下面一層個數+中間一層個數+最上面一層個數＝4+4+4＝12；
第3個幾何體：最下面一層個數+中間兩層個數+最上面一層個數＝4+8+8＝20；
……
總結規律，回答下列問題：
(1)第4個幾何體中只有兩個面涂色的小立方體共有   ▲  個；
(2)第n個幾何體中只有兩個面涂色的小立方體共有多少個？（用含字母n的式子表示.）

Answer 1

（1）28，（2）8n-4

（1）28. ………………2分
（2）觀察圖形可知：圖①中，兩面涂色的小立方體共有4個；
圖②中，兩面涂色的小立方體共有12個；
圖③中，兩面涂色的小立方體共有20個．
4，12，20都是4的倍數，可分別寫成4×1，4×3，4×5的形式，
因此，第n個圖中兩面涂色的小立方體共有4（2n-1）=8n-4
（1）第1個幾何體中最底層的4個角的小立方體只有2個面涂色；第4個幾何體中只有2個面涂色的小立方體共有7×4=28個；
（2）根據所給圖形中只有2個面涂色的小立方體的塊數得到第n個幾何體中只有2個面涂色的小立方體的塊數與4的倍數的關系即可；