
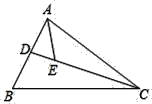
【題目】在△ABC中,∠ADC=88°,∠B=68°,∠ACD=∠BCD,AE平分∠BAC,則∠AED的度數為_____.
科目:初中數學 來源: 題型:
【題目】已知一次函數y=kx+b的圖象過P(1,4),Q(4,1)兩點,且與x軸交于A點.
(1)求此一次函數的解析式;
(2)求△POQ的面積;
(3)已知點M在x軸上,若使MP+MQ的值最小,
求點M的坐標及MP+MQ的最小值.

查看答案和解析>>
科目:初中數學 來源: 題型:
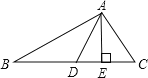
【題目】已知如圖所示 AD、AE分別是△ABC的中線、高,且AB=5cm,AC=3cm,,則△ABD與△ACD的周長之差為_________,△ABD與△ACD的面積關系為_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩校參加區教育局舉辦的學生英語口語競賽,兩校參賽人數相等.比賽結束后,發現學生成績分別為7分、8分、9分、10分(滿分為10分).依據統計數據繪制了如下尚不完整的統計圖表. 

(1)在圖1中,“7分”所在扇形的圓心角等于°.
(2)請你將圖2的統計圖補充完整;
(3)經計算,乙校的平均分是8.3分,中位數是8分,請寫出甲校的平均分、中位數;并從平均分和中位數的角度分析哪個學校成績較好.
(4)如果該教育局要組織8人的代表隊參加市級團體賽,為便于管理,決定從這兩所學校中的一所挑選參賽選手,請你分析,應選哪所學校?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現代互聯網技術的廣泛應用,催生了快遞行業的高速發展.小明計劃給朋友快遞一部分物品,經了解有甲、乙兩家快遞公司比較合適.甲公司表示:快遞物品不超過1千克的,按每千克22元收費;超過1千克,超過的部分按每千克15元收費.乙公司表示:按每千克16元收費,另加包裝費3元.設小明快遞物品x千克.
(1)請分別寫出甲、乙兩家快遞公司快遞該物品的費用y(元)與x(千克)之間的函數關系式;
(2)小明選擇哪家快遞公司更省錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠ABC=90°,以AB為直徑的⊙O交AC于點D,E為BC邊的中點,連接DE. 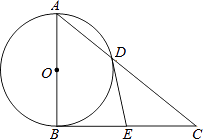
(1)求證:DE與⊙O相切.
(2)若tanC= ![]() ,DE=2,求AD的長.
,DE=2,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,對角線AC=2 ![]() ,E為BC邊上一點,BC=3BE,將矩形ABCD沿AE所在的直線折疊,B點恰好落在對角線AC上的B′處,則AB= .
,E為BC邊上一點,BC=3BE,將矩形ABCD沿AE所在的直線折疊,B點恰好落在對角線AC上的B′處,則AB= .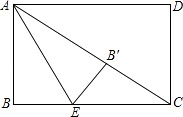
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將一張矩形紙板按圖中虛線裁剪成九塊,其中有兩塊是邊長都為![]() 的大正方形,兩塊是邊長都為
的大正方形,兩塊是邊長都為![]() 的小正方形,五塊是長為
的小正方形,五塊是長為![]() 、寬為
、寬為![]() 的全等小矩形,且
的全等小矩形,且![]() >
> ![]() .(以上長度單位:cm)
.(以上長度單位:cm)
(1)觀察圖形,可以發現代數式![]() 可以因式分解為 ;
可以因式分解為 ;
(2)若每塊小矩形的面積為10![]() ,四個正方形的面積和為58
,四個正方形的面積和為58![]() ,試求圖中所有裁剪線(虛線部分)長之和.
,試求圖中所有裁剪線(虛線部分)長之和.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC中,∠BAC=90°,AB=AC,點D為直線BC上一動點(點D不與B,C重合),以AD為邊在AD右側作正方形ADEF,連接CF.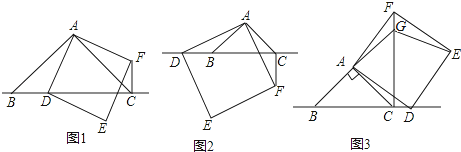
(1)觀察猜想
如圖1,當點D在線段BC上時,
①BC與CF的位置關系為: .
②BC,CD,CF之間的數量關系為:;(將結論直接寫在橫線上)
(2)數學思考
如圖2,當點D在線段CB的延長線上時,結論①,②是否仍然成立?若成立,請給予證明;若不成立,請你寫出正確結論再給予證明.
(3)拓展延伸
如圖3,當點D在線段BC的延長線上時,延長BA交CF于點G,連接GE.若已知AB=2 ![]() ,CD=
,CD= ![]() BC,請求出GE的長.
BC,請求出GE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com