
【題目】如圖,點![]() 在直線
在直線![]() 上,過點
上,過點![]() 作
作![]() ,且
,且![]() ,點
,點![]() 在射線
在射線![]() 上(點
上(點![]() 不與點
不與點![]() 重合),且滿足
重合),且滿足![]() ,
,![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() .設(shè)
.設(shè)![]()
![]() .
.
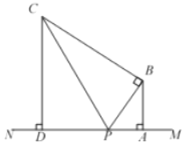
(1)用含![]() 的代數(shù)式表示
的代數(shù)式表示![]() 的長;
的長;
(2)①線段![]() 的長是________;
的長是________;
②線段![]() 的長是_________;(用含
的長是_________;(用含![]() 的代數(shù)式表示)
的代數(shù)式表示)
(3)當(dāng)![]() 為何值時,
為何值時,![]() 有最小值?并求出這個最小值.
有最小值?并求出這個最小值.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() ;(3)
;(3)![]() 時,
時,![]() 的最小值
的最小值![]() .
.
【解析】
(1)首先證明![]() ,然后根據(jù)相似三角形性質(zhì)進(jìn)一步得出
,然后根據(jù)相似三角形性質(zhì)進(jìn)一步得出![]() ,再結(jié)合勾股定理所得的
,再結(jié)合勾股定理所得的![]() 進(jìn)一步對式子進(jìn)行分析求解即可;
進(jìn)一步對式子進(jìn)行分析求解即可;
(2)①延長![]() 和
和![]() 交于點
交于點![]() ,通過證明
,通過證明![]() ,由此進(jìn)一步得出
,由此進(jìn)一步得出![]() ,然后再證明出
,然后再證明出![]() ,最后利用相似三角形性質(zhì)求出CD即可;②先證明
,最后利用相似三角形性質(zhì)求出CD即可;②先證明![]() ,據(jù)此進(jìn)一步得出
,據(jù)此進(jìn)一步得出![]() ,由此得出
,由此得出![]() ,最后進(jìn)一步證明
,最后進(jìn)一步證明![]() ,從而得出答案即可;
,從而得出答案即可;
(3)過點![]() 作
作![]() 于點
于點![]() ,通過證明
,通過證明![]() ,由此得出
,由此得出![]() ,然后得出
,然后得出![]() ,根據(jù)當(dāng)點
,根據(jù)當(dāng)點![]() 運動時,總有
運動時,總有![]() ,所以當(dāng)點
,所以當(dāng)點![]() 與點
與點![]() 重合,即
重合,即![]() 時,
時,![]() 的最小值
的最小值![]() ,由此求出
,由此求出![]() 的最小值,最后根據(jù)題意進(jìn)一步求出
的最小值,最后根據(jù)題意進(jìn)一步求出![]() 即可.
即可.
(1)在![]() 和
和![]() 中,
中,
∵![]() ,
,![]() 90°,
90°,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
又根據(jù)勾股定理可得:![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)
①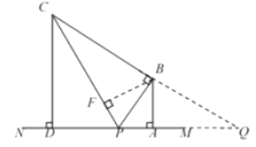
如圖,延長![]() 和
和![]() 交于點
交于點![]() ,
,
∵![]() ,
,![]() ,且
,且![]() ,
,
∴![]() ,則有
,則有![]() ,即
,即![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
②∵![]() ,
,![]() ,
,
∴∠ABP+∠APB=∠ABP+∠ABQ=90°,
∴∠APB=∠ABQ,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
由①知![]() ,結(jié)合
,結(jié)合![]() 可得:
可得:![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案為:①8;②![]() ;
;
(3)
如圖,過點![]() 作
作![]() 于點
于點![]() ,
,
∵∠BAP=∠BFP,∠APB=∠FPB,PB=PB,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴當(dāng)點![]() 運動時,總有
運動時,總有![]() ,
,
∴當(dāng)點![]() 與點
與點![]() 重合,即
重合,即![]() 時,
時,![]() 的最小值
的最小值![]() ,
,
則![]() 的最小值
的最小值![]() .
.
此時,如圖所示,
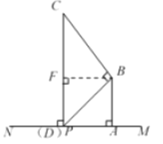
其中![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() (不符合題意,舍去).
(不符合題意,舍去).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學(xué) 來源: 題型:
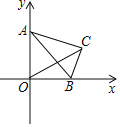
【題目】如圖,在平面直角坐標(biāo)系中,點![]() 為坐標(biāo)原點,將含30°角的
為坐標(biāo)原點,將含30°角的![]() 放在第一象限,其中30°角的對邊
放在第一象限,其中30°角的對邊![]() 長為1,斜邊
長為1,斜邊![]() 的端點
的端點![]() ,
,![]() 分別在
分別在![]() 軸的正半軸,
軸的正半軸,![]() 軸的正半軸上滑動,連接
軸的正半軸上滑動,連接![]() ,則線段
,則線段![]() 的長的最大值是( )
的長的最大值是( )
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
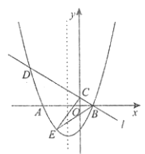
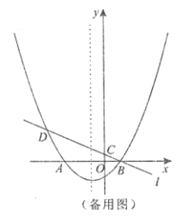
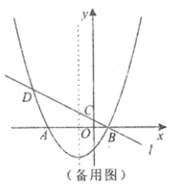
【題目】如圖,已知拋物線![]() 與
與![]() 軸交于點
軸交于點![]() 、
、![]() (點
(點![]() 在點
在點![]() 的左側(cè)),經(jīng)過點
的左側(cè)),經(jīng)過點![]() 的直線
的直線![]() :
:![]() 與
與![]() 軸交于點
軸交于點![]() ,與拋物線的另一個交點為
,與拋物線的另一個交點為![]() .
.
(1)則點![]() 的坐標(biāo)為__________,點
的坐標(biāo)為__________,點![]() 的坐標(biāo)為__________,拋物線的對稱軸為__________;
的坐標(biāo)為__________,拋物線的對稱軸為__________;
(2)點![]() 是直線
是直線![]() 下方拋物線上的一點,當(dāng)
下方拋物線上的一點,當(dāng)![]() 時.求
時.求![]() 面積的最大值;
面積的最大值;
(3)設(shè)![]() 為拋物線對稱軸上一點,點
為拋物線對稱軸上一點,點![]() 在拋物線上,若以點
在拋物線上,若以點![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形為矩形,求
為頂點的四邊形為矩形,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】隨著交通道路的不斷完善,帶動了旅游業(yè)的發(fā)展,某市旅游景區(qū)有A、B、C、D、E等著名景點,該市旅游部門統(tǒng)計繪制出2017年“五一”長假期間旅游情況統(tǒng)計圖,根據(jù)以下信息解答下列問題:

(1)2017年“五一”期間,該市周邊景點共接待游客 萬人,扇形統(tǒng)計圖中A景點所對應(yīng)的圓心角的度數(shù)是 ,并補(bǔ)全條形統(tǒng)計圖.
(2)根據(jù)近幾年到該市旅游人數(shù)增長趨勢,預(yù)計2018年“五一”節(jié)將有80萬游客選擇該市旅游,請估計有多少萬人會選擇去E景點旅游?
(3)甲、乙兩個旅行團(tuán)在A、B、D三個景點中,同時選擇去同一景點的概率是多少?請用畫樹狀圖或列表法加以說明,并列舉所用等可能的結(jié)果.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】王老師在數(shù)學(xué)課上帶領(lǐng)同學(xué)們做數(shù)學(xué)游戲,規(guī)則如下:
游戲規(guī)則
甲任報一個有理數(shù)數(shù)傳給乙;
乙把這個數(shù)減![]() 后報給丙;
后報給丙;
丙再把所得的數(shù)的絕對值報給丁;
丁再把這個數(shù)的一半減![]() ,報出答案.
,報出答案.
根據(jù)游戲規(guī)則,回答下面的問題:
(1)若甲報的數(shù)為![]() ,則乙報的數(shù)為_________,丁報出的答案是_________;
,則乙報的數(shù)為_________,丁報出的答案是_________;
(2)若甲報的數(shù)為![]() ,請列出算式并計算丁報出的答案;
,請列出算式并計算丁報出的答案;
(3)若丁報出的答案是![]() ,則直接寫出甲報的數(shù).
,則直接寫出甲報的數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】開學(xué)初期,天氣炎熱,水杯需求量大.雙福育才中學(xué)門口某超市購進(jìn)一批水杯,其中A種水杯進(jìn)價為每個15元,售價為每個25元;B種水杯進(jìn)價為每個12元,售價為每個20元
(1)該超市平均每天可售出60個A種水杯,后來經(jīng)過市場調(diào)查發(fā)現(xiàn),A種水杯單價每降低1元,則平均每天的銷量可增加10個.為了盡量讓學(xué)生得到更多的優(yōu)惠,某天該超市將A種水杯售價調(diào)整為每個m元,結(jié)果當(dāng)天銷售A種水杯獲利630元,求m的值.
(2)該超市準(zhǔn)備花費不超過1600元的資金,購進(jìn)A、B兩種水杯共120個,其中B種水杯的數(shù)量不多于A種水杯數(shù)量的兩倍.請為該超市設(shè)計獲利最大的進(jìn)貨方案,并求出最大利潤.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在矩形 ABCD 中,M,N,P,Q 分別為邊 AB,BC,CD,DA 上的點(不與端點重合).對于任意矩形 ABCD,下面四個結(jié)論中:①存在無數(shù)個四邊形 MNPQ 是平行四邊形;②存在無數(shù)個四邊形 MNPQ 是矩形;③存在無數(shù)個四邊形 MNPQ 是菱形;④不存在四邊形 MNPQ 是正方形.所有正確結(jié)論的序號是_________________ .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在矩形![]() 中,
中,![]() ,
,![]() ,以點
,以點![]() 為坐標(biāo)原點,
為坐標(biāo)原點,![]() 所在的直線為
所在的直線為![]() 軸,建立直角坐標(biāo)系.
軸,建立直角坐標(biāo)系.

(Ⅰ)將矩形![]() 繞點
繞點![]() 逆時針旋轉(zhuǎn)至矩形
逆時針旋轉(zhuǎn)至矩形![]() ,如圖1,
,如圖1,![]() 經(jīng)過點
經(jīng)過點![]() ,求旋轉(zhuǎn)角的大小和點
,求旋轉(zhuǎn)角的大小和點![]() ,
,![]() 的坐標(biāo);
的坐標(biāo);
(Ⅱ)將圖1中矩形![]() 沿直線
沿直線![]() 向左平移,如圖2,平移速度是每秒1個單位長度.
向左平移,如圖2,平移速度是每秒1個單位長度.
①經(jīng)過幾秒,直線![]() 經(jīng)過點
經(jīng)過點![]() ;
;
②設(shè)兩矩形重疊部分的面積為![]() ,運動時間為
,運動時間為![]() ,寫出重疊部分面積
,寫出重疊部分面積![]() 與時間
與時間![]() 之間的函數(shù)關(guān)系式.
之間的函數(shù)關(guān)系式.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,一次函數(shù)![]() 的圖像分別交x、y軸于點A、B,拋物線
的圖像分別交x、y軸于點A、B,拋物線![]() 經(jīng)過點A、B,點P為第四象限內(nèi)拋物線上的一個動點.
經(jīng)過點A、B,點P為第四象限內(nèi)拋物線上的一個動點.
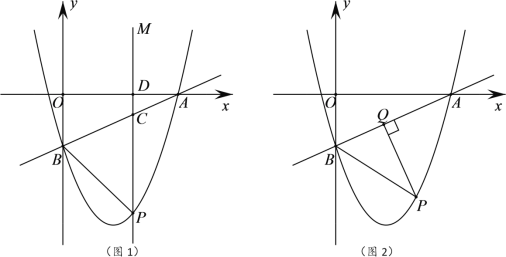
(1)求此拋物線對應(yīng)的函數(shù)表達(dá)式;
(2)如圖1所示,過點P作PM∥y軸,分別交直線AB、x軸于點C、D,若以點P、B、C為頂點的三角形與以點A、C、D為頂點的三角形相似,求點P的坐標(biāo);
(3)如圖2所示,過點P作PQ⊥AB于點Q,連接PB,當(dāng)△PBQ中有某個角的度數(shù)等于∠OAB度數(shù)的2倍時,請直接寫出點P的橫坐標(biāo).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com