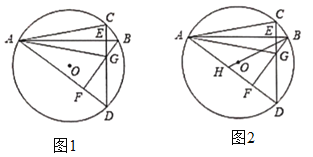
【題目】已知
是圓
的兩條弦，
于
，連接
，過點
作
，垂足為
.
（1）如圖1，連接
，求證：
；
（2）如圖2，連接
并延長交于點
，若
平分
，求圓的半徑和
的長.
【答案】（1）見解析；（2）圓O的半徑2.5；
【解析】
（1）連接BC，如圖，根據已知條件易得∠D=∠ABG，進而利用全等三角形的判定定理證明△BCE≌△BGE，接下來根據全等三角形的性質，利用線段垂直平分線的性質即可證得結論；
（2）連接CO并延長交⊙O于M，連接AM，可得
，由已知AG=4，可得AM、AC的值，根據勾股定理求出CM，即可得圓O的半徑；過點H作HN⊥AB，過點O作OP⊥AB，如圖，聯系三角函數的知識、角平分線的性質及勾股定理進行推理，即可求出AH的長.
連接
，
，
，
.
弧
弧
，
，
，
，
.
，
，
，
，
；
（2）如圖，連接
并延長交
于
，連接
，
是圓的直徑，
.
弧弧，
，
.
，
，
在
中，
，
，
，
圓的半徑為
，
過
作
于
，可得
，
.
在
中，
，
設
，則
，
平分
.
在
中，
，
，
在
中，
，
過作
于
，則
.
，
，
.
故答案為：（1）見解析；（2）圓O的半徑2.5；.
科目：初中數學 來源： 題型：
【題目】如圖，在矩形ABCD中，AB＝4，AD＝6，E是AB邊的中點，F是線段BC上的動點，將△EBF沿EF所在直線折疊得到△EB′F，連接B′D，則B′D的最小值是（ ）
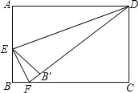
A. 2
﹣2B. 6C. 2
﹣2D. 4
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】若關于x的一元二次方程（m+1）x2﹣2x﹣1＝0有兩個不相等的實數根，
（1）求m的取值范圍；
（2）若x＝1是方程的一個根，求m的值和另一個根．
查看答案和解析>>
科目：初中數學 來源： 題型：
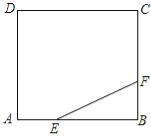
【題目】如圖，正方形ABCD的邊長為3，點E，F分別在邊AB、BC上，AE=BF=1，小球P從點E出發沿直線向點F運動，每當碰到正方形的邊時反彈，反彈時反射角等于入射角．當小球P第一次碰到點E時，小球P所經過的路程為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
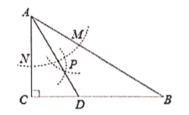
【題目】如圖，在
中，
，以
為圓心，任意長為半徑畫弧分別交
于點
和
，再分別以
為圓心，大于
的長為半徑畫弧，兩弧交于點
，連結
并延長交
于點
，則下列說法中正確的個數是（）
①點到
的兩邊距離相等；
②點在
的中垂線上；
③
④
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，要在寬為22米的大道兩邊安裝路燈，路燈的燈臂CD長2米，且與燈柱BC成120°角，路燈采用圓錐形燈罩，燈罩的軸線DO與燈臂CD垂直，當燈罩的軸線DO通過公路路面的中心線時照明效果最佳，求路燈的燈柱BC高度．
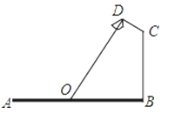
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲乙兩人勻速從同一地點到1500米處的圖書館看書，甲出發5分鐘后，乙以50米/分的速度沿同一路線行走.設甲乙兩人相距
（米），甲行走的時間為
（分），
關于
的函數函數圖像的一部分如圖所示.
（1）求甲行走的速度；
（2）在坐標系中，補畫
關于
函數圖象的其余部分；
（3）問甲、乙兩人何時相距360米？
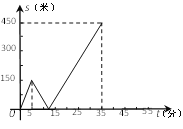
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在直角坐標系中，矩形OABC的頂點O與坐標原點重合，A、C分別在坐標軸上，點B的坐標為（4，2），直線
交AB，BC分別于點M，N，反比例函數
的圖象經過點M，N．
（1）求反比例函數的解析式；
（2）若點P在y軸上，且△OPM的面積與四邊形BMON的面積相等，求點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一次函數
的圖像與反比例函數
(k＞0)的圖像交于A，B兩點，過點A做x軸的垂線，垂足為M，△AOM面積為1.
（1）求反比例函數的解析式；
（2）在y軸上求一點P,使PA+PB的值最小，并求出其最小值和P點坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com