
【題目】如圖AM∥BN,C是BN上一點, BD平分∠ABN且過AC的中點O,交AM于點D,DE⊥BD,交BN于點E.
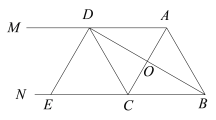
(1)求證:△ADO≌△CBO.
(2)求證:四邊形ABCD是菱形.
(3)若DE = AB = 2,求菱形ABCD的面積.
【答案】(1)見解析;(2)見解析;(3)![]()
【解析】
(1)由ASA即可得出結論;
(2)先證明四邊形ABCD是平行四邊形,再證明AD=AB,即可得出結論;
(3)由菱形的性質得出AC⊥BD,證明四邊形ACED是平行四邊形,得出AC=DE=2,AD=EC,由菱形的性質得出EC=CB=AB=2,得出EB=4,由勾股定理得BD═![]() ,即可得出答案.
,即可得出答案.
(1)∵點O是AC的中點,
∴AO=CO,
∵AM∥BN,
∴∠DAC=∠ACB,
在△AOD和△COB中,
 ,
,
∴△ADO≌△CBO(ASA);
(2)由(1)得△ADO≌△CBO,
∴AD=CB,
又∵AM∥BN,
∴四邊形ABCD是平行四邊形,
∵AM∥BN,
∴∠ADB=∠CBD,
∵BD平分∠ABN,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AD=AB,
∴平行四邊形ABCD是菱形;
(3)由(2)得四邊形ABCD是菱形,
∴AC⊥BD,AD=CB,
又DE⊥BD,
∴AC∥DE,
∵AM∥BN,
∴四邊形ACED是平行四邊形,
∴AC=DE=2,AD=EC,
∴EC=CB,
∵四邊形ABCD是菱形,
∴EC=CB=AB=2,
∴EB=4,
在Rt△DEB中,由勾股定理得BD=![]() =
=![]() ,
,
∴![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點C是圓周上一點,連接AC、BC,以點C為端點作射線CD、CP分別交線段AB所在直線于點D、P,使∠1=∠2=∠A.

(1)求證:直線PC是⊙O的切線;
(2)若CD=4,BD=2,求線段BP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
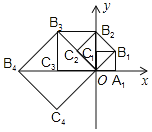
【題目】如圖,在平面直角坐標系中,邊長為1的正方形![]() 的兩邊在坐標軸上,以它的對角線
的兩邊在坐標軸上,以它的對角線![]() 為邊作正方形
為邊作正方形![]() ,再以正方形
,再以正方形![]() 的對角線
的對角線![]() 為邊作正方形
為邊作正方形![]() ,以此類推
,以此類推![]() 、則正方形
、則正方形![]() 的頂點
的頂點![]() 的坐標是______.
的坐標是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校初三進行了第三次模擬考試,該校領導為了了解學生的數學考試情況,抽樣調查部分學生的數學成績,并將抽樣的數據進行了如下整理:
①如下分數段整理樣本;
等級等級 | 分數段 | 各組總分 | 人數 |
A | 110<X<120 | P | 4 |
B | 100<X<110 | 843 | n |
C | 90<X≤100 | 574 | m |
D | 80<X<90 | 171 | 2 |
②根據左表繪制扇形統計圖.

(1)填空m= ,n= ,數學成績的中位數所在的等級 ;
(2)如果該校有1200名學生參加了本次模擬測,估計D等級的人數;
(3)已知抽樣調查學生的數學成績平均分為102分,求A等級學生的數學成績的平均分數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,有下列結論:①abc>0;②2a+b=0;③若m為任意實數,則a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,則x1+x2=2.其中,正確結論的個數為( )
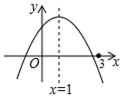
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某區初二年級數學學科期末質量監控情況,進行了抽樣調查,過程如下,請將有關問題補充完整.收集數據:隨機抽取甲乙兩所學校的名學生的數學成績進行
甲 91 89 77 86 71 31 97 93 72 91 81 92 85 85 95 88 88 90 44 91
乙 84 93 66 69 76 87 77 82 85 88 90 88 67 88 91 96 68 97 59 88
整理、描述數據:按如下數據段整理、描述這兩組數據,分析數據:
分段 學校 |
|
|
|
|
|
|
|
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 |
兩組數據的平均數、中位數、眾數、方差如下表:
統計量 學校 | 平均數 | 中位數 | 眾數 | 方差 |
甲 | 81.85 |
| 91 | 268.43 |
乙 | 81.95 | 86 | 88 | 115.25 |
(1)經統計,表格中![]() 的值是__________.
的值是__________.
(2)得出結論
①若甲學校有600名初二學生,估計這次考試成績80分以上人數為__________.
②可以推斷出__________學校學生的數學水平較高,理由為:__________.(至少從兩個不同的角度說明推斷的合理性)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,AE⊥BC,AF⊥CD,垂足分別為E,F,且BE=DF.
(1)求證:ABCD是菱形;
(2)若AB=5,AC=6,求ABCD的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了給游客提供更好的服務,某景區隨機對部分游客進行了關于“景區服務工作滿意度”的調查,并根據調查結果繪制成如下不完整的統計圖表.
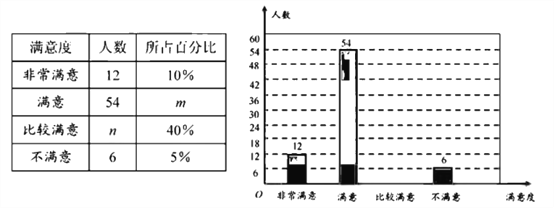
根據圖表信息,解答下列問題:
(1)本次調查的總人數為 ,表中![]() 的值為 ;
的值為 ;
(2)請補全條形統計圖;
(3)據統計,該景區平均每天接待游客約3600人,若將“非常滿意”和“滿意”作為游客對景區服務工作的肯定,請你估計該景區服務工作平均每天得到多少名游客的肯定.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】國內豬肉價格不斷上漲,已知今年10月的豬肉價格比今年年初上漲了80%,李奶奶10月在某超市購買1千克豬肉花了72元錢.
(1)今年年初豬肉的價格為每千克多少元?
(2)某超市將進貨價為每千克55元的豬肉按10月價格出售,平均一天能銷售出100千克,隨著國家對豬肉價格的調控,超市發現豬肉的售價每千克下降1元,其日銷售量就增加10千克,超市為了實現銷售豬肉每天有1800元的利潤,并且盡可能讓顧客得到實惠,豬肉的售價應該下降多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com