
【題目】如圖,在ABCD中,![]() ,
,![]() ,
,![]() ,點(diǎn)E為CD上一動點(diǎn),經(jīng)過A、C、E三點(diǎn)的
,點(diǎn)E為CD上一動點(diǎn),經(jīng)過A、C、E三點(diǎn)的![]() 交BC于點(diǎn)F.
交BC于點(diǎn)F.
(操作與發(fā)現(xiàn))
![]() 當(dāng)E運(yùn)動到
當(dāng)E運(yùn)動到![]() 處,利用直尺與規(guī)作出點(diǎn)E與點(diǎn)F;
處,利用直尺與規(guī)作出點(diǎn)E與點(diǎn)F;![]() 保留作圖痕跡
保留作圖痕跡![]()
![]() 在
在![]() 的條件下,證明:
的條件下,證明:![]() .
.
(探索與證明)
![]() 點(diǎn)E運(yùn)動到任何一個位置時,求證:
點(diǎn)E運(yùn)動到任何一個位置時,求證:![]() ;
;
(延伸與應(yīng)用)
![]() 點(diǎn)E在運(yùn)動的過程中求EF的最小值.
點(diǎn)E在運(yùn)動的過程中求EF的最小值.

【答案】![]() 作圖見解析;
作圖見解析;![]() 證明見解析;
證明見解析;![]() 證明見解析;
證明見解析;![]() EF最小值為
EF最小值為![]() .
.
【解析】
![]() 當(dāng)
當(dāng)![]() ,此時AC是
,此時AC是![]() 的直徑,作出AC的中點(diǎn)O后,以OA為半徑作出
的直徑,作出AC的中點(diǎn)O后,以OA為半徑作出![]() 即可作出點(diǎn)E、F;
即可作出點(diǎn)E、F;
![]() 易知AC為直徑,則
易知AC為直徑,則![]() ,
,![]() ,從而得證;
,從而得證;
![]() 如圖,作
如圖,作![]() ,
,![]() ,若E在DN之間,由
,若E在DN之間,由![]() 可知,
可知,![]() ,然后再證明
,然后再證明![]() ∽
∽![]() ,從而可知
,從而可知![]() ,若E在CN之間時,同理可證;
,若E在CN之間時,同理可證;
![]() 由于A、F、C、E四點(diǎn)共圓,所以
由于A、F、C、E四點(diǎn)共圓,所以![]() ,由于四邊形ABCD為平行四邊形,
,由于四邊形ABCD為平行四邊形,![]() ,從而可證
,從而可證![]() 為等腰直角三角形,所以
為等腰直角三角形,所以![]() ,由于
,由于![]() ,所以E與N重合時,FE最小.
,所以E與N重合時,FE最小.
![]() 如圖1所示,
如圖1所示,

![]() 如圖,易知AC為直徑,則
如圖,易知AC為直徑,則![]() ,
,
則![]() ,
,
![]() ,
,
![]() 如圖,作
如圖,作![]() ,
,![]() ,若E在DN之間
,若E在DN之間
由![]() 可知,
可知,![]()
![]() 、F、C、E四點(diǎn)共圓,
、F、C、E四點(diǎn)共圓,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ∽
∽![]()
![]() ,
,
若E在CN之間時,同理可證
![]() 、F、C、E四點(diǎn)共圓,
、F、C、E四點(diǎn)共圓,
![]() ,
,
![]() 四邊形ABCD為平行四邊形,
四邊形ABCD為平行四邊形,![]() ,
,

![]() ,
,
![]() ,
,
![]() ,
,
![]() 為等腰直角三角形,
為等腰直角三角形,
![]() ,
,
![]() ,
,
![]() 與N重合時,FE最小,
與N重合時,FE最小,
此時![]() ,
,
在![]() 中,
中,![]() ,則
,則![]()
![]() 由勾股定理可知:
由勾股定理可知:![]()
此時EF最小值為![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩車從A地出發(fā),沿同一路線駛向B地.甲車先出發(fā)勻速駛向B地,40min后,乙車出發(fā),勻速行駛一段時間后,在途中的貨站裝貨耗時半小時.由于滿載貨物,為了行駛安全,速度減少了50km/h,結(jié)果與甲車同時到達(dá)B地.甲乙兩車距A地的路程y(km)與乙車行駛時間x(h)之間的函數(shù)圖象如圖所示,則下列說法中正確的有( )
①![]() ;②甲的速度是60km/h;③乙出發(fā)80min追上甲;④乙剛到達(dá)貨站時,甲距B地180km.
;②甲的速度是60km/h;③乙出發(fā)80min追上甲;④乙剛到達(dá)貨站時,甲距B地180km.

A.4個B.3個C.2個D.1個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在菱形ABCD中,AB=4,E為BC中點(diǎn),AE⊥BC于點(diǎn)E,AF⊥CD于點(diǎn)F,CG∥AE,CG交AF于點(diǎn)H,交AD于點(diǎn)G.
(1)求菱形ABCD的面積;(2)求∠CHA的度數(shù).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】圖①是一個長為2m、寬為2n的長方形,沿圖中虛線用剪刀均分成四塊小長方形,然后按圖②的形狀拼成一個正方形.(1)請用兩種不同的方法求圖②中陰影部分的面積:
方法1: 方法2:
(2)觀察圖②請你寫出下列三個代數(shù)式:(m+n)2,(m﹣n)2,mn之間的等量關(guān)系. ;
(3)根據(jù)(2)題中的等量關(guān)系,解決:已知:a﹣b=5,ab=﹣6,求:(a+b)2的值;

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
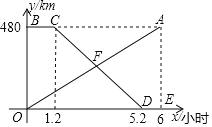
【題目】甲、乙兩地相距480km,一輛貨車從甲地勻速駛往乙地,貨車出發(fā)一段時間后,一輛汽車從乙地勻速駛往甲地,設(shè)貨車行駛的時間為![]() 線段OA表示貨車離甲地的距離
線段OA表示貨車離甲地的距離![]() 與xh的函數(shù)圖象;折線BCDE表示汽車距離甲地的距離
與xh的函數(shù)圖象;折線BCDE表示汽車距離甲地的距離![]() 與
與![]() 的函數(shù)圖象.
的函數(shù)圖象.
![]() 求線段OA與線段CD所表示的函數(shù)表達(dá)式;
求線段OA與線段CD所表示的函數(shù)表達(dá)式;
![]() 若OA與CD相交于點(diǎn)F,求點(diǎn)F的坐標(biāo),并解釋點(diǎn)F的實(shí)際意義;
若OA與CD相交于點(diǎn)F,求點(diǎn)F的坐標(biāo),并解釋點(diǎn)F的實(shí)際意義;
![]() 當(dāng)x為何值時,兩車相距100千米?
當(dāng)x為何值時,兩車相距100千米?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.

(1)求證:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的長度.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】我們有時會碰上形如![]() ,
,![]() ,
,![]() 的式子,其實(shí)我們可以將其進(jìn)一步分母有理化.
的式子,其實(shí)我們可以將其進(jìn)一步分母有理化.
形如![]() 的式子還可以用以下方法化簡:
的式子還可以用以下方法化簡:![]() .(*)
.(*)
(1)請用不同的方法化簡(寫出化簡過程):
(i)參照分母有理化的方法得![]() ______________________________;
______________________________;
(ii)參照(*)式的化簡方法得![]() ______________________________.
______________________________.
(2)化簡:![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,矩形ABCD的面積為1cm2,對角線交于點(diǎn)O;以AB、AO為鄰邊作平行四邊形AOC1B,對角線交于點(diǎn)O1;以AB、AO1為鄰邊作平行四邊形AO1C2B…;依此類推,則平行四邊形AO2016C2017B的面積為_____.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com