
【題目】“低碳環保,綠色出行”的理念得到廣大群眾的接受,越來越多的人再次選擇自行車作為出行工具,小軍和爸爸同時從家騎自行車去圖書館,爸爸先以150米/分的速度騎行一段時間,休息了5分鐘,再以m米/分的速度到達圖書館,小軍始終以同一速度騎行,兩人行駛的路程y(米)與時間x(分鐘)的關系如圖,請結合圖象,解答下列問題: 
(1)a= , b= , m= ;
(2)若小軍的速度是120米/分,求小軍在途中與爸爸第二次相遇時,距圖書館的距離;
(3)在(2)的條件下,爸爸自第二次出發至到達圖書館前,何時與小軍相距100米?
(4)若小軍的行駛速度是v米/分,且在途中與爸爸恰好相遇兩次(不包括家、圖書館兩地),請直接寫出v的取值范圍.
【答案】
(1)10;15;200
(2)解:線段BC所在直線的函數解析式為y=1500+200(x﹣15)=200x﹣1500;
線段OD所在的直線的函數解析式為y=120x.
聯立兩函數解析式成方程組,
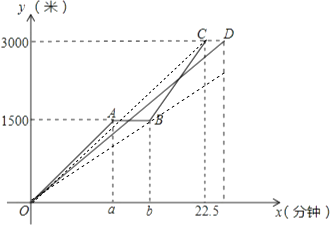
![]() ,解得:
,解得: 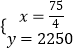 ,
,
∴3000﹣2250=750(米).
答:小軍在途中與爸爸第二次相遇時,距圖書館的距離是750米.
(3)解:根據題意得:|200x﹣1500﹣120x|=100,
解得:x1= ![]() =17.5,x2=20.
=17.5,x2=20.
答:爸爸自第二次出發至到達圖書館前,17.5分鐘時和20分鐘時與小軍相距100米.
(4)解:當線段OD過點B時,小軍的速度為1500÷15=100(米/分鐘);
當線段OD過點C時,小軍的速度為3000÷22.5= ![]() (米/分鐘).
(米/分鐘).
結合圖形可知,當100<v< ![]() 時,小軍在途中與爸爸恰好相遇兩次(不包括家、圖書館兩地).
時,小軍在途中與爸爸恰好相遇兩次(不包括家、圖書館兩地).
【解析】解:(1)1500÷150=10(分鐘), 10+5=15(分鐘),
(3000﹣1500)÷(22.5﹣15)=200(米/分).
故答案為:10;15;200.
(1)根據時間=路程÷速度,即可求出a值,結合休息的時間為5分鐘,即可得出b值,再根據速度=路程÷時間,即可求出m的值;(2)根據數量關系找出線段BC、OD所在直線的函數解析式,聯立兩函數解析式成方程組,通過解方程組求出交點的坐標,再用3000去減交點的縱坐標,即可得出結論;(3)根據(2)結論結合二者之間相距100米,即可得出關于x的含絕對值符號的一元一次方程,解之即可得出結論;(4)分別求出當OD過點B、C時,小軍的速度,結合圖形,利用數形結合即可得出結論.


科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系,O為坐標原點,點A(﹣1,0),點B(0, ![]() ).
).
(1)求∠BAO的度數;
(2)如圖1,將△AOB繞點O順時針得△A′OB′,當A′恰好落在AB邊上時,設△AB′O的面積為S1 , △BA′O的面積為S2 , S1與S2有何關系?為什么?
(3)若將△AOB繞點O順時針旋轉到如圖2所示的位置,S1與S2的關系發生變化了嗎?證明你的判斷.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將邊長為3的正方形![]() 置于平面直角坐標系第一象限,使邊
置于平面直角坐標系第一象限,使邊![]() 落在
落在![]() 軸的正半軸上,直線
軸的正半軸上,直線![]() :
:![]() 經過點
經過點![]() 且與
且與![]() 軸交于點
軸交于點![]() .
.

(1)求![]() 點坐標;
點坐標;
(2)求![]() 的面積;
的面積;
(3)若直線![]() 與
與![]() 軸交于點
軸交于點![]() ,在
,在![]() 軸上是否存在點
軸上是否存在點![]() ,使得
,使得![]() 是直角三角形?若存在,請直接寫出點
是直角三角形?若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場計劃購進一批甲、乙兩種玩具,已知一件甲種玩具的進價與一件乙種玩具的進價的和為40元,用90元購進甲種玩具的件數與用150元購進乙種玩具的件數相同.
(1)求每件甲種、乙種玩具的進價分別是多少元?
(2)商場計劃購進甲、乙兩種玩具共48件,其中甲種玩具的件數少于乙種玩具的件數,商場決定此次進貨的總資金不超過1000元,求商場共有幾種進貨方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,AC與BD相交于點O,∠AOB=60°,BD=4,將△ABC沿直線AC翻折后,點B落在點E處,那么S△AED=______

查看答案和解析>>
科目:初中數學 來源: 題型:
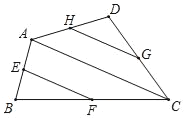
【題目】如圖,點E、F、G、H分別是四邊形ABCD的邊AB、BC、CD、DA的中點.
(1)如果圖中線段都可畫成有向線段,那么在這些有向線段所表示的向量中,與向量![]() 相等的向量是 ;
相等的向量是 ;
(2)設![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() .試用向量
.試用向量![]() ,
,![]() 或
或![]() 表示下列向量:
表示下列向量:![]() = ;
= ;![]() = .
= .
(3)求作:![]()
![]() .(請在原圖上作圖,不要求寫作法,但要寫出結論)
.(請在原圖上作圖,不要求寫作法,但要寫出結論)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用長度一定的不銹鋼材料設計成外觀為矩形的框架(如圖①②中的一種).設豎檔AB=x米,請根據以上圖案回答下列問題:(題中的不銹鋼材料總長均指各圖中所有黑線的長度和,所有橫檔和豎檔分別與AD、AB平行)
(1)在圖①中,如果不銹鋼材料總長度為12米,當x為多少時,矩形框架ABCD的面積為3平方米?
(2)在圖②中,如果不銹鋼材料總長度為12米,當x為多少時,矩形框架ABCD的面積S最大?最大面積是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com