
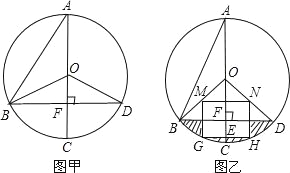
【題目】如圖甲,已知在⊙O中,AB=![]() ,AC是⊙O的直徑,AC⊥BD于F,∠A=30度.
,AC是⊙O的直徑,AC⊥BD于F,∠A=30度.
(1)連接BC,CD,請你判定四邊形OBCD是何種特殊的四邊形?試說明理由;
(2)若用扇形OBD圍成一個圓錐側面,請求出這個圓錐的底面圓的半徑;
(3)如圖乙,若將“∠A=30°”改為“∠A=22.5°”,其余條件不變,以半徑OB、OD的中點M、N為頂點作矩形MNGH,頂點G、H在⊙O的劣弧![]() 上,GH交OC于點E.試求圖中陰影部分的面積.(結果保留π)
上,GH交OC于點E.試求圖中陰影部分的面積.(結果保留π)
【答案】(1)四邊形OBCD是菱形,證明見解析;(2)![]() ;(3)
;(3)![]() ;
;
【解析】
(1)根據(jù)對角線互相垂直的平行四邊形是菱形進行證明,由AC⊥BD,根據(jù)垂徑定理可知:BF=FD,故只需證明OF=CF.在Rt△ABF中,已知∠A和AB,可將BF,AF的長求出;在Rt△BOF中,運用勾股定理可將半徑OB及OF求出,根據(jù)CF=2OB-AF可將CF求出,根據(jù)OF=CF,BF=FD,BD⊥OC,可證四邊形OBCD為菱形;
(2)已知扇形BOD的圓心角和半徑,代入l弧長=![]() 進行求解,再根據(jù)底面周長:2πr=l弧長,可求出圓錐底面的半徑;
進行求解,再根據(jù)底面周長:2πr=l弧長,可求出圓錐底面的半徑;
(3)作輔助線,連接OH,S陰影=S扇形OBD-S△BOD-S下矩形,S扇形=![]() lR,S△BOD=
lR,S△BOD=![]() OB2,代入數(shù)據(jù)可將扇形AOB和△BOD的面積求出,由M、N是△OBD的中位線,可知MN=
OB2,代入數(shù)據(jù)可將扇形AOB和△BOD的面積求出,由M、N是△OBD的中位線,可知MN=![]() BD,在Rt△OEH中,根據(jù)勾股定理可求出OE,又OF=
BD,在Rt△OEH中,根據(jù)勾股定理可求出OE,又OF=![]() OB,可得EF=OE-OF,故:S下矩形=MN×EF,從而可將陰影部分的面積求出.
OB,可得EF=OE-OF,故:S下矩形=MN×EF,從而可將陰影部分的面積求出.
解:(1)四邊形OBCD是菱形.
如圖丙,∵AC⊥BD,AC是直徑,
∴AC垂直平分BD.
∴BF=FD,![]() .
.
∴∠BAD=2∠BAC=60°,
∴∠BOD=120°.
∵BF=![]() AB=2
AB=2![]() ,
,
在Rt△ABF中,
AF=![]() ,
,
在Rt△BOF中,
∴OB2=BF2+OF2.即![]() .
.
解得:OB=4.
∵OA=OB=4,
∴OF=AF﹣AO=6﹣4=2,
∵AC=2OA=8,
∴CF=AC﹣AF=8﹣6=2,
∴CF=OF,
∵BF=FD,AC⊥BD,
∴四邊形OBCD是菱形;
(2)設圓錐的底面圓的半徑為r,則周長為2πr.
∵扇形OBD的弧長=![]() ,
,
∴![]() ,
,
解得:r=![]() ;
;
(3)如圖丁,連接OH.
∵∠A=22.5°,
∴∠BOC=45°,
∵∠BOD=∠BOC=90°
設半徑OB=r,由勾股定理則有![]()
化簡得r2=24(2﹣![]() )
)
∵M、N是OB、OD的中點,
∵四邊形MNGH是矩形,
∴MN2=GH2=12(2﹣![]() ),EH2=EG2=
),EH2=EG2=![]() MN2=3(2﹣
MN2=3(2﹣![]() ).
).
在Rt△HOE中,OE2=OH2﹣HE2,即OE2=r2﹣3(2﹣![]() ),
),
解得:OE2=21(2﹣![]() ),
),
∴下矩形的面積=(OE﹣OF)×MN=![]() ,
,
∵扇形OBD的面積=![]() ,
,
∴圖中陰影部分的面積=![]() -
-![]()
=![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】如圖所示,點![]() 是線段
是線段![]() 的中點,
的中點,![]() ,
,![]() .
.
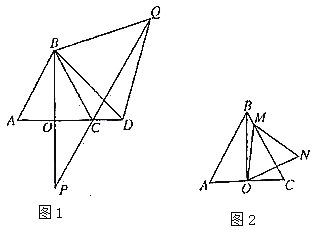
(1)如圖1,若![]() ,求證
,求證![]() 是等邊三角形;
是等邊三角形;
(2)如圖1,在(1)的條件下,若點![]() 在射線
在射線![]() 上,點
上,點![]() 在點
在點![]() 右側,且
右側,且![]() 是等邊三角形,
是等邊三角形,![]() 的延長線交直線
的延長線交直線![]() 于點
于點![]() ,求
,求![]() 的長度;
的長度;
(3)如圖2,在(1)的條件下,若點![]() 在線段
在線段![]() 上,
上,![]() 是等邊三角形,且點
是等邊三角形,且點![]() 沿著線段
沿著線段![]() 從點
從點![]() 運動到點
運動到點![]() ,點
,點![]() 隨之運動,求點
隨之運動,求點![]() 的運動路徑的長度.
的運動路徑的長度.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點P的坐標為(0,4),直線y=![]() x-3與x軸、y軸分別交于點A、B,點M是直線AB上的一個動點,則PM的最小值為________.
x-3與x軸、y軸分別交于點A、B,點M是直線AB上的一個動點,則PM的最小值為________.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,直角坐標系xOy中,一次函數(shù)y=﹣![]() x+5的圖象l1分別與x,y軸交于A,B兩點,正比例函數(shù)的圖象l2與l1交于點C(m,4).
x+5的圖象l1分別與x,y軸交于A,B兩點,正比例函數(shù)的圖象l2與l1交于點C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函數(shù)y=kx+1的圖象為l3,且11,l2,l3不能圍成三角形,直接寫出k的值.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,AB是半圓O的直徑,C、D是半圓O上的兩點,且OD∥BC,OD與AC交于點E.
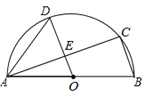
(1)若∠B=70°,求弧CD的度數(shù);
(2)若AB=26,DE=8,求AC的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
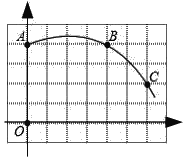
【題目】如圖,網(wǎng)格紙中每個小正方形的邊長為1,一段圓弧經(jīng)過格點,點O為坐標原點.
(1)該圖中弧所在圓的圓心D的坐標為 ;.
(2)根據(jù)(1)中的條件填空:
①圓D的半徑= (結果保留根號);
②點(7,0)在圓D (填“上”、“內(nèi)”或“外”);
③∠ADC的度數(shù)為 .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某市甲、乙兩個汽車銷售公司,去年一至十月份每月銷售同種品牌汽車的情況如圖所示:
![]() 請你根據(jù)上圖填寫下表:
請你根據(jù)上圖填寫下表:
銷售公司 | 平均數(shù) | 方差 | 中位數(shù) | 眾數(shù) |
甲 |
| 9 | ||
乙 | 9 |
| 8 |
![]() 請你從以下兩個不同的方面對甲、乙兩個汽車銷售公司去年一至十月份的銷售情況進行分析:
請你從以下兩個不同的方面對甲、乙兩個汽車銷售公司去年一至十月份的銷售情況進行分析:
![]() 從平均數(shù)和方差結合看;
從平均數(shù)和方差結合看;
![]() 從折線圖上甲、乙兩個汽車銷售公司銷售數(shù)量的趨勢看
從折線圖上甲、乙兩個汽車銷售公司銷售數(shù)量的趨勢看![]() 分析哪個汽車銷售公司較有潛力
分析哪個汽車銷售公司較有潛力![]() .
.

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com