
【題目】如圖所示,△ABE和△ADC是△ABC分別沿著AB,AC邊翻折180°形成的,若∠1:∠2:∠3=28:5:3,則∠α的度數為( ) 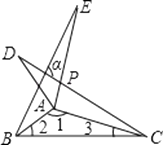
A.80°
B.100°
C.60°
D.45°
【答案】A
【解析】解:設∠3=3x,則∠1=28x,∠2=5x, ∵∠1+∠2+∠3=180°,
∴28x+5x+3x=180°,解得x=5°,
∴∠1=140°,∠2=25°,∠3=15°,
∵△ABE是△ABC沿著AB邊翻折180°形成的,
∴∠1=∠BAE=140°,∠E=∠3=15°,
∴∠EAC=360°﹣∠BAE﹣∠BAC=360°﹣140°﹣140°=80°,
又∵△ADC是△ABC沿著AC邊翻折180°形成的,
∴∠ACD=∠E=15°,
而∠α+∠E=∠EAC+∠ACD,
∴∠α=∠EAC=80°.
故選A.
先根據三角形的內角和定理易計算出∠1=140°,∠2=25°,∠3=15°,根據折疊的性質得到∠1=∠BAE=140°,∠E=∠3=15°,∠ACD=∠E=15°,可計算出∠EAC,然后根據∠α+∠E=∠EAC+∠ACD,即可得到∠α=∠EAC.


科目:初中數學 來源: 題型:
【題目】下列命題中,真命題是( )
A.兩條對角線相等的四邊形是矩形
B.兩條對角線互相垂直的四邊形是菱形
C.兩條對角線互相垂直且相等的四邊形是正方形
D.兩條對角線互相平分的四邊形是平行四邊形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】規律探究.下面有8個算式,排成4行2列
2+2, 2×2
3+ ![]() , 3×
, 3× ![]()
4+ ![]() , 4×
, 4× ![]()
5+ ![]() , 5×
, 5× ![]() ……, ……
……, ……
(1)同一行中兩個算式的結果怎樣?
(2)算式2005+ ![]() 和2005×
和2005× ![]() 的結果相等嗎?
的結果相等嗎?
(3)請你試寫出算式,試一試,再探索其規律,并用含自然數n的代數式表示這一規律.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖在數軸上A點表示數a,B點表示數b,a、b滿足|a+2|+|b﹣4|=0.![]()
(1)點A表示的數為;點B表示的數為;
(2)一小球甲從點A處以1個單位/秒的速度向左運動;同時另一小球乙從點B處以2個單位/秒的速度也向左運動,設運動的時間為t(秒),
①當t=1時,甲小球到原點的距離為;乙小球到原點的距離為;當t=3時,甲小球到原點的距離為;乙小球到原點的距離為;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小松調查了七年級(1)班50名同學最喜歡的籃球明星,結果如下:
B B C A A B C D C B C A D D B A C C B A
A B D A C C A B A C A B C D A C C A C A
A A A C A D B C C A
其中A代表科比,B代表庫里,C代表詹姆斯,D代表格里芬,用扇形統計圖表示該班同學最喜歡的籃球明星的情況,則表示喜歡科比的扇形的圓心角是(用度分秒表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果P 是正方形ABCD 內的一點,且滿足∠APB+∠DPC=180°,那么稱點P 是正方形 ABCD 的“對補點”.
(1)如圖1,正方形ABCD 的對角線AC,BD 交于點M,求證:點M 是正方形ABCD 的對補點;
(2)如圖2,在平面直角坐標系中,正方形ABCD 的頂點A(1,1),C(3,3).除對角線交點外,請再寫出一個該正方形的對補點的坐標,并證明.
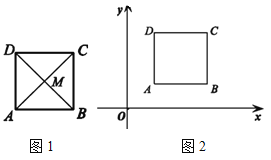
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知四邊形ABCD中,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN繞B點旋轉,它的兩邊分別交AD,DC(或它們的延長線)于E,F. 當∠MBN繞B點旋轉到AE=CF時(如圖1),易證AE+CF=EF;
當∠MBN繞B點旋轉到AE≠CF時,在圖2和圖3這兩種情況下,上述結論是否成立?若成立,請給予證明;若不成立,線段AE,CF,EF又有怎樣的數量關系?請寫出你的猜想,不需證明.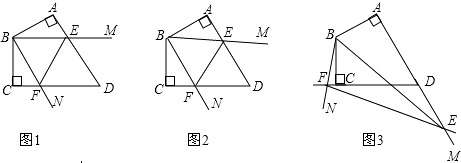
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,O是直線AB上一點,OC為任一條射線,OM平分∠AOC,ON平分∠BOC.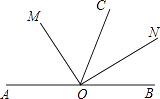
(1)圖中與∠AON互補的角有;
(2)猜想∠MON的度數為 , 試說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com