
【題目】已知,直線AB∥DC,點P為平面上一點,連接AP與CP.
(1)如圖1,點P在直線AB、CD之間,當∠BAP=60°,∠DCP=20°時,求∠APC.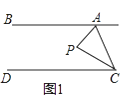
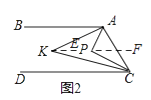
(2)如圖2,點P在直線AB、CD之間,∠BAP與∠DCP的角平分線相交于點K,寫出∠AKC與∠APC之間的數量關系,并說明理由.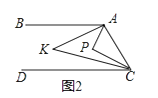
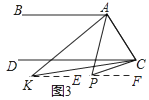
(3)如圖3,點P落在CD外,∠BAP與∠DCP的角平分線相交于點K,∠AKC與∠APC有何數量關系?并說明理由.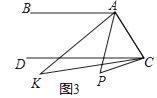
【答案】
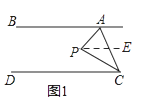
(1)解:如圖1,過P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠APE=∠BAP,∠CPE=∠DCP,
∴∠APC=∠APE+∠CPE=∠BAP+∠DCP=60°+20°=80°;
(2)解:∠AKC= ![]() ∠APC.
∠APC.
理由:如圖2,過K作KE∥AB,
∵AB∥CD,
∴KE∥AB∥CD,
∴∠AKE=∠BAK,∠CKE=∠DCK,
∴∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,
過P作PF∥AB,
同理可得,∠APC=∠BAP+∠DCP,
∵∠BAP與∠DCP的角平分線相交于點K,
∴∠BAK+∠DCK= ![]() ∠BAP+
∠BAP+ ![]() ∠DCP=
∠DCP= ![]() (∠BAP+∠DCP)=
(∠BAP+∠DCP)= ![]() ∠APC,
∠APC,
∴∠AKC= ![]() ∠APC;
∠APC;
(3)解:∠AKC= ![]() ∠APC.
∠APC.
理由:如圖3,過K作KE∥AB,
∵AB∥CD,
∴KE∥AB∥CD,
∴∠BAK=∠AKE,∠DCK=∠CKE,
∴∠AKC=∠AKE﹣∠CKE=∠BAK﹣∠DCK,
過P作PF∥AB,
同理可得,∠APC=∠BAP﹣∠DCP,
∵∠BAP與∠DCP的角平分線相交于點K,
∴∠BAK﹣∠DCK= ![]() ∠BAP﹣
∠BAP﹣ ![]() ∠DCP=
∠DCP= ![]() (∠BAP﹣∠DCP)=
(∠BAP﹣∠DCP)= ![]() ∠APC,
∠APC,
∴∠AKC= ![]() ∠APC.
∠APC.
【解析】(1)先過P作PE∥AB,根據平行線的性質即可得到∠APE=∠BAP,∠CPE=∠DCP,再根據∠APC=∠APE+∠CPE=∠BAP+∠DCP進行計算即可;(2)過K作KE∥AB,平行公理的推理可得到KE∥AB∥CD,可得∠AKE=∠BAK,∠CKE=∠DCK,進而得到∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,同理可得,∠APC=∠BAP+∠DCP,再根據角平分線的定義得出∠BAK+∠DCK=![]() ∠BAP+
∠BAP+![]() ∠DCP,進而可得到問題的答案;
∠DCP,進而可得到問題的答案;
(3)過K作KE∥AB,依據平行公理的推理可得到KE∥AB∥CD,可得∠BAK=∠AKE,∠DCK=∠CKE,進而得到∠AKC=∠AKE-∠CKE=∠BAK-∠DCK,同理可得,∠APC=∠BAP-∠DCP,再根據角平分線的定義,得出∠BAK-∠DCK=![]() ∠BAP-
∠BAP-![]() ∠DCP=
∠DCP=![]() (∠BAP-∠DCP)=
(∠BAP-∠DCP)=![]() ∠APC,進而得到∠AKC=
∠APC,進而得到∠AKC=![]() ∠APC.
∠APC.
【考點精析】認真審題,首先需要了解平行線的性質(兩直線平行,同位角相等;兩直線平行,內錯角相等;兩直線平行,同旁內角互補).


科目:初中數學 來源: 題型:
【題目】小軒從如圖所示的二次函數y=ax2+bx+c(a≠0)的圖象中,觀察得出了下面五條信息:
①ab>0;②a+b+c<0;③b+2c>0;④a﹣2b+4c>0;⑤![]() .
.
你認為其中正確信息的個數有( )
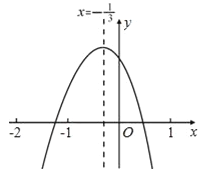
A.2個 B.3個 C.4個 D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著空氣質量的惡化,霧霾天氣現象增多,危害加重.森林是“地球之肺”,每年能為人類提供大約28.3億噸的有機物,28.3億可用科學記數法表示為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,小方格邊長為1個單位,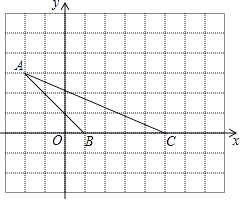
(1)請寫出△ABC各點的坐標.
(2)求出S△ABC .
(3)若把△ABC向上平移2個單位,再向右平移2個單位△A′B′C′,在圖中畫出△A′B′C′.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某品牌的共享自行車企業為了解工作日期間地鐵站附近的自行車使用情況,做到精確投放,于星期二當天對荔灣區A、B、C三個地鐵站該品牌自行車后使用量進行了統計,繪制如圖1和圖2所示的統計圖,根據圖中信息解答下列問題: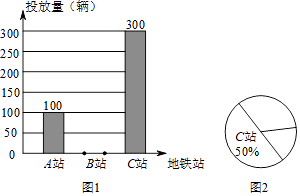
(1)該品牌自行車當天在該三個地鐵站區域投放了自行車輛.
(2)請補全圖1中的條形統計圖;求出地鐵A站在圖2中所對應的圓心角的度數.
(3)按統計情況,若該品牌車計劃在這些區域再投放1200輛,估計在地鐵B站應投入多少輛.
查看答案和解析>>
科目:初中數學 來源: 題型:
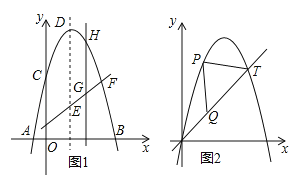
【題目】如圖1所示,已知拋物線![]() 的頂點為D,與x軸交于A、B兩點,與y軸交于C點,E為對稱軸上的一點,連接CE,將線段CE繞點E按逆時針方向旋轉90°后,點C的對應點C′恰好落在y軸上.
的頂點為D,與x軸交于A、B兩點,與y軸交于C點,E為對稱軸上的一點,連接CE,將線段CE繞點E按逆時針方向旋轉90°后,點C的對應點C′恰好落在y軸上.
(1)直接寫出D點和E點的坐標;
(2)點F為直線C′E與已知拋物線的一個交點,點H是拋物線上C與F之間的一個動點,若過點H作直線HG與y軸平行,且與直線C′E交于點G,設點H的橫坐標為m(0<m<4),那么當m為何值時,![]() =5:6?
=5:6?
(3)圖2所示的拋物線是由![]() 向右平移1個單位后得到的,點T(5,y)在拋物線上,點P是拋物線上O與T之間的任意一點,在線段OT上是否存在一點Q,使△PQT是等腰直角三角形?若存在,求出點Q的坐標;若不存在,請說明理由.
向右平移1個單位后得到的,點T(5,y)在拋物線上,點P是拋物線上O與T之間的任意一點,在線段OT上是否存在一點Q,使△PQT是等腰直角三角形?若存在,求出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法中的錯誤的是( ).
A、一組鄰邊相等的矩形是正方形
B、一組鄰邊相等的平行四邊形是菱形
C、一組對邊相等且有一個角是直角的四邊形是矩形
D、一組對邊平行且相等的四邊形是平行四邊形
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com