
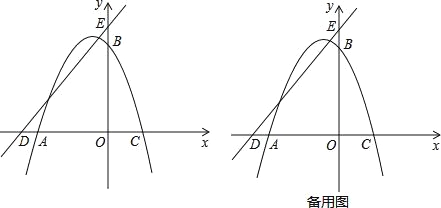
【題目】如圖,在平面直角坐標系中,O為坐標原點,拋物線y=ax2+2xa+c經過A(﹣4,0),B(0,4)兩點,與x軸交于另一點C,直線y=x+5與x軸交于點D,與y軸交于點E.
(1)求拋物線的解析式;
(2)點P是第二象限拋物線上的一個動點,連接EP,過點E作EP的垂線l,在l上截取線段EF,使EF=EP,且點F在第一象限,過點F作FM⊥x軸于點M,設點P的橫坐標為t,線段FM的長度為d,求d與t之間的函數關系式(不要求寫出自變量t的取值范圍);
(3)在(2)的條件下,過點E作EH⊥ED交MF的延長線于點H,連接DH,點G為DH的中點,當直線PG經過AC的中點Q時,求點F的坐標.
【答案】(1)![]() ;(2)d=5+t;(3)F
;(2)d=5+t;(3)F![]() .
.
【解析】
試題分析:(1)直接把A、B坐標代入求出a、c得值即可;(2)分別過P、F向y軸作垂線,垂足分別為A′、B′,過P作PN⊥x軸,垂足為N,易證△PEA′≌△EFB′,可得出d=FM=OE﹣EB′,再代入可求得解析式;(3)先求得F、H的坐標,發現點P和點H的縱坐標相等,則PH與x軸平行,根據平行線截線段成比例定理可得G也是PQ的中點,由此表示出點G的坐標并列式,求出t的值并取舍,計算出點F的坐標.
試題解析:(1)由題意得![]() ,解得
,解得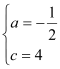 ,∴拋物線解析式為
,∴拋物線解析式為![]() ;(2)分別過P、F向y軸作垂線,垂足分別為A′、B′,過P作PN⊥x軸,垂足為N,當x=0時,y=5,∴E(0,5),∴OE=5,∵∠PEO+∠OEF=90°,∠PEO+∠EPA′=90°,∴∠EPA′=∠OEF,∵PE=EF,∠EA′P=∠EB′F=90°,∴△PEA′≌△EFB′,∴PA′=EB′=﹣t,∴d=FM=OB′=OE﹣EB′=5﹣(﹣t)=5+t;
;(2)分別過P、F向y軸作垂線,垂足分別為A′、B′,過P作PN⊥x軸,垂足為N,當x=0時,y=5,∴E(0,5),∴OE=5,∵∠PEO+∠OEF=90°,∠PEO+∠EPA′=90°,∴∠EPA′=∠OEF,∵PE=EF,∠EA′P=∠EB′F=90°,∴△PEA′≌△EFB′,∴PA′=EB′=﹣t,∴d=FM=OB′=OE﹣EB′=5﹣(﹣t)=5+t;
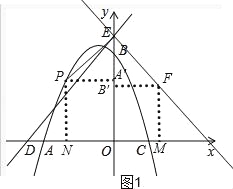
(3)如圖,由直線DE的解析式為:y=x+5,∵EH⊥ED,∴直線EH的解析式為:y=﹣x+5,
∴FB′=A′E=5﹣(﹣![]() t2﹣t+4)=
t2﹣t+4)=![]() t2+t+1,∴F(
t2+t+1,∴F(![]() t2+t+1,5+t),∴點H的橫坐標為:
t2+t+1,5+t),∴點H的橫坐標為:![]() t2+t+1,
t2+t+1,
y=﹣![]() t2﹣t﹣1+5=﹣
t2﹣t﹣1+5=﹣![]() t2﹣t+4,∴H(
t2﹣t+4,∴H(![]() t2+t+1,﹣
t2+t+1,﹣![]() t2﹣t+4),∵G是DH的中點,∴G(
t2﹣t+4),∵G是DH的中點,∴G(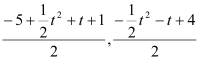 ),即G(
),即G(![]() t2+
t2+![]() t﹣2,﹣
t﹣2,﹣![]() t2﹣
t2﹣![]() t+2),∴PH∥x軸,∵DG=GH,∴PG=GQ,
t+2),∴PH∥x軸,∵DG=GH,∴PG=GQ,
∴![]() ,解得t=
,解得t=![]() ,∵P在第二象限,∴t<0,∴t=
,∵P在第二象限,∴t<0,∴t=![]() ,∴F(
,∴F(![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
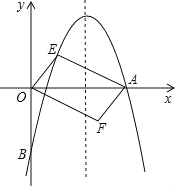
【題目】如圖,對稱軸為直線x=的拋物線經過點A(6,0)和B(0,﹣4).
(1)求拋物線解析式及頂點坐標;
(2)設點E(x,y)是拋物線上一動點,且位于第一象限,四邊形OEAF是以OA為對角線的平行四邊形,求平行四邊形OEAF的面積S與x之間的函數關系式;
(3)當(2)中的平行四邊形OEAF的面積為24時,請判斷平行四邊形OEAF是否為菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
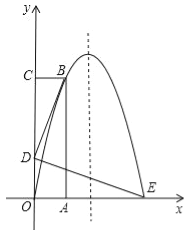
【題目】如圖,長方形OABC的OA邊在x軸的正半軸上,OC在y軸的正半軸上,拋物線y=ax2+bx經過點B(1,4)和點E(3,0)兩點.
(1)求拋物線的解析式;
(2)若點D在線段OC上,且BD⊥DE,BD=DE,求D點的坐標;
(3)在條件(2)下,在拋物線的對稱軸上找一點M,使得△BDM的周長為最小,并求△BDM周長的最小值及此時點M的坐標;
(4)在條件(2)下,從B點到E點這段拋物線的圖象上,是否存在一個點P,使得△PAD的面積最大?若存在,請求出△PAD面積的最大值及此時P點的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com