
【題目】如圖,每個小正方形的邊長都是1, 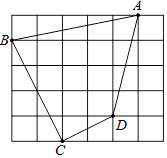
(1)求四邊形ABCD的周長和面積;
(2)∠BCD是直角嗎?
【答案】
(1)解:AB= ![]() ,AD=
,AD= ![]() ,CD=
,CD= ![]() ,BC=2
,BC=2 ![]() ,
,
四邊形ABCD的周長為 ![]() ;
;
面積為5×5﹣ ![]() ×1×5﹣
×1×5﹣ ![]() ×1×4﹣1﹣
×1×4﹣1﹣ ![]() ×1×2﹣
×1×2﹣ ![]() ×2×4=14.5
×2×4=14.5
(2)解:連接BD,
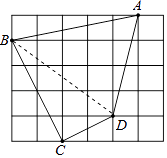
∵BC=2 ![]() ,CD=
,CD= ![]() ,BD=5,
,BD=5,
∴BC2+CD2=BD2,
∴△BCD是直角三角形,
∴∠BCD是直角.
【解析】(1)利用勾股定理求出AB、BC、CD和DA的長,即可求出四邊形ABCD的周長;利用分割法即可求出四邊形的面積;(2)連接BD,求出BD的長,利用勾股定理的逆定理即可證明出結論.
【考點精析】認真審題,首先需要了解勾股定理的概念(直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2),還要掌握勾股定理的逆定理(如果三角形的三邊長a、b、c有下面關系:a2+b2=c2,那么這個三角形是直角三角形)的相關知識才是答題的關鍵.


科目:初中數學 來源: 題型:
【題目】小明和小慧兩位同學在數學活動課中,把長為30cm,寬為10cm的長方形白紙條粘合起來,小明按如圖甲所示的方法粘合起來得到長方形ABCD,粘合部分的長度為6cm,小慧按如圖乙所示的方法粘合起來得到長方形A1B1C1D1,黏合部分的長度為4cm.若長為30cm,寬為10cm的長方形白紙條共有100張,則小明應分配到 張長方形白紙條,才能使小明和小慧按各自要求黏合起來的長方形面積相等(要求100張長方形白紙條全部用完).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,直線![]() ,與x軸、y軸分別交于點A、C,以AC為對角線作矩形OABC,點P、Q分別為射線OC、射線AC上的動點,且有AQ=2CP, 連結PQ,設點P的坐標為P(0,t).
,與x軸、y軸分別交于點A、C,以AC為對角線作矩形OABC,點P、Q分別為射線OC、射線AC上的動點,且有AQ=2CP, 連結PQ,設點P的坐標為P(0,t).
(1)求點B的坐標.
(2)若t=1時,連接BQ,求△ABQ的面積.
(3)如圖2,以PQ為直徑作⊙I,記⊙I與射線AC的另一個交點為E.
① 若![]() ,求此時t的值.
,求此時t的值.
② 若圓心I在△ABC內部(不包含邊上),則此時t的取值范圍為 .(直接寫出答案)
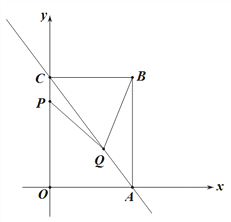
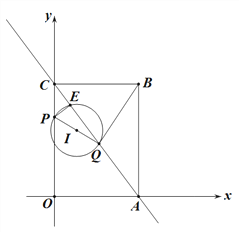
圖1 圖2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com