
【題目】如圖,已知二次函數y=﹣ ![]() +bx+c的圖象經過A(2,0)、B(0,﹣6)兩點.
+bx+c的圖象經過A(2,0)、B(0,﹣6)兩點.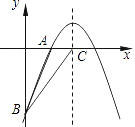
(1)求這個二次函數的解析式;
(2)設該二次函數的對稱軸與x軸交于點C,連接BA,BC,求△ABC的面積.
【答案】
(1)
解:把A(2,0)、B(0,﹣6)代入y=﹣ ![]() +bx+c,
+bx+c,
得: ![]()
解得 ![]() ,
,
∴這個二次函數的解析式為y=﹣ ![]() +4x﹣6
+4x﹣6
(2)
解:∵該拋物線對稱軸為直線x=﹣ ![]() =4,
=4,
∴點C的坐標為(4,0),
∴AC=OC﹣OA=4﹣2=2,
∴S△ABC= ![]() ×AC×OB=
×AC×OB= ![]() ×2×6=6
×2×6=6
【解析】(1)二次函數圖象經過A(2,0)、B(0,﹣6)兩點,兩點代入y=﹣ ![]() +bx+c,算出b和c,即可得解析式.(2)先求出對稱軸方程,寫出C點的坐標,計算出AC,然后由面積公式計算值.
+bx+c,算出b和c,即可得解析式.(2)先求出對稱軸方程,寫出C點的坐標,計算出AC,然后由面積公式計算值.
【考點精析】認真審題,首先需要了解二次函數的圖象(二次函數圖像關鍵點:1、開口方向2、對稱軸 3、頂點 4、與x軸交點 5、與y軸交點).


科目:初中數學 來源: 題型:
【題目】已知正方形ABCD中,E為對角線BD上一點,過E點作EF⊥BD交BC于F,連接DF,G為DF中點,連接EG,CG.
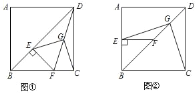
(1)求證:EG=CG;
(2)將圖①中△BEF繞B點逆時針旋轉45°,如圖②所示,取DF中點G,連接EG,CG.
問(1)中的結論是否仍然成立?若成立,請給出證明;若不成立,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC中,AB=AC,∠BAC=90°.
(1)如圖,若CD平分∠ACB,BE⊥CD,垂足E在CD的延長線上,試探究線段BE和CD的數量關系,并證明你的結論
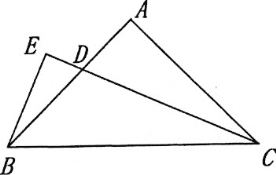
(2)如圖,若點D在線段BC延長上,BE⊥DE,垂足為E,DE與AB相交于點F.試探究線段BE和FD的數量關系,并證明你的結論.
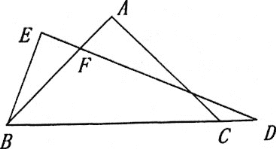
查看答案和解析>>
科目:初中數學 來源: 題型:
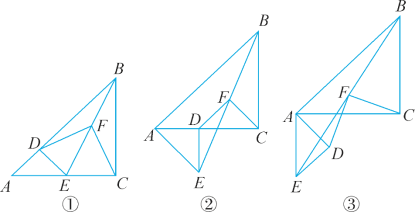
【題目】已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,F為BE的中點,連結DF,CF.
(1)如圖①,當點D在AB上,點E在AC上,請直接寫出此時線段DF,CF的數量關系和位置關系.
(2)如圖②,在(1)的條件下將△ADE繞點A順時針旋轉45°,請你判斷此時(1)中的結論是否仍然成立,并證明你的判斷.
(3)如圖③,在(1)的條件下將△ADE繞點A順時針旋轉90°,若AD=1,AC=![]() ,求此時線段CF的長(直接寫出結果).
,求此時線段CF的長(直接寫出結果).
查看答案和解析>>
科目:初中數學 來源: 題型:
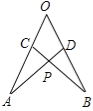
【題目】如圖:在∠AOB的兩邊截取OA=OB,OC=OD,連接AD,BC交于點P,則下列結論中①△AOD≌△BOC,②△APC≌△BPD,③點P在∠AOB的平分線上。 正確的是 (填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正比例函數y=﹣2x與反比例函數y= ![]() 的圖象相交于A(m,2),B兩點.
的圖象相交于A(m,2),B兩點. 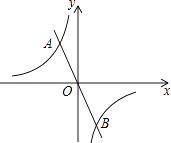
(1)求反比例函數的表達式及點B的坐標;
(2)結合圖象直接寫出當﹣2x> ![]() 時,x的取值范圍.
時,x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解某市120000名初中學生的視力情況,某校數學興趣小組收集有關數據,并進行整理分析.
(1)小明在眼鏡店調查了1000名初中學生的視力,小剛在鄰居中調查了20名初中學生的視力,他們的抽樣是否合理?并說明理由.
(2)該校數學興趣小組從該市七、八、九年級各隨機抽取了1000名學生進行調查,整理他們的視力情況數據,得到如下的折線統計圖. 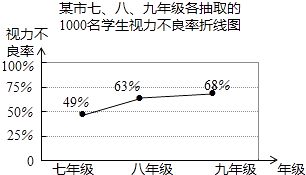
請你根據抽樣調查的結果,估計該市120000名初中學生視力不良的人數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AC=BC,AB是⊙C的切線,切點為D,直線AC交⊙C于點E、F,且CF= ![]() AC.
AC. 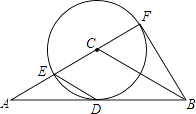
(1)求∠ACB的度數;
(2)若AC=8,求△ABF的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com