
【題目】已知線段AB=4.8cm,C是線段AB的中點,D是線段CB的中點,點E在AB上,且CE=![]() AC,則DE的長為_____.
AC,則DE的長為_____.
【答案】2cm或0.4cm
【解析】
分點E在線段AC上及點E在線段BC上兩種情況考慮:(1)當點E在線段AC上時,根據AB的長度及點C、D分別是線段AB、CB的中點,即可得出CD、CE的長度,將其代入DE=CD+CE中即可求出DE的長;(2)當點E在線段CB上時,根據AB的長度及點C、D分別是線段AB、CB的中點,即可得出CD、CE的長度,將其代入DE=CD﹣CE中即可求出DE的長.綜上即可得出結論.
(1)當點E在線段AC上時,如圖1所示.
![]()
∵AB=4.8cm,點C是線段AB的中點,
∴AC=BC=![]() AB=2.4cm.
AB=2.4cm.
∵點D是線段CB的中點,
∴CD=![]() BC=1.2cm.
BC=1.2cm.
又∵CE=![]() AC,
AC,
∴CE=0.8cm,
∴DE=CD+CE=1.2+0.8=2(cm).
(2)當點E在線段BC上時,如圖2所示.
![]()
∵AB=4.8cm,點C是線段AB的中點,
∴AC=BC=![]() AB=2.4cm.
AB=2.4cm.
∵點D是線段CB的中點,
∴CD=![]() BC=1.2cm.
BC=1.2cm.
又∵CE=![]() AC,
AC,
∴CE=0.8cm,
∴DE=CD﹣CE=1.2﹣0.8=0.4(cm).
綜上所述:DE的長為2cm或0.4cm,
故答案為:2cm或0.4cm.


科目:初中數學 來源: 題型:
【題目】已知數軸上兩點A,B對應的數分別是﹣10,8,P,Q,N為數軸上三個動點,點P從點A出發速度為每秒2個單位,點Q從點B出發,速度為點P的2倍,點N從原點出發,速度為每秒1個單位.
(1)若P,Q兩點不動,動點N是線段AB的三等分點時,點N所表示的數是 ;
(2)若點P向左運動,同時點Q向右運動,求多長時間點P與點Q相距32個單位?
(3)若點P,Q,N同時都向右運動求多長時間點N到點P和點Q的距離相等?
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面內有四個點A,B,C,D. 根據下列語句畫圖:
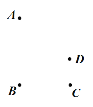
①畫直線BC;
②畫射線AD交直線![]() 于點E;
于點E;
③連接BD,用圓規在線段BD的延長線上截取DF=BD;
④在圖中確定點O,使點O到點A,B,C,D的距離之和最小.
(友情提醒:截取用圓規,并保留痕跡;畫完圖要下結論)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于數軸上的A,B,C三點,給出如下定義:若其中一個點與其它兩個點的距離恰好滿足2倍的數量關系,則稱該點是其它兩個點的“聯盟點”.
例如數軸上點A,B,C所表示的數分別為1,3,4,此時點B是點A, C的“聯盟點”.
![]()
(1)若點A表示數-2, 點B表示的數2,下列各數![]() ,0,4,6所對應的點分別C1,C2 ,C3 ,C4,其中是點A,B的“聯盟點”的是 ;
,0,4,6所對應的點分別C1,C2 ,C3 ,C4,其中是點A,B的“聯盟點”的是 ;
(2)點A表示數-10, 點B表示的數30,P在為數軸上一個動點:
①若點P在點B的左側,且點P是點A, B的“聯盟點”,求此時點P表示的數;
②若點P在點B的右側,點P,A, B中,有一個點恰好是其它兩個點的“聯盟點”,寫出此時點P表示的數 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】課外活動時間,甲、乙、丙、丁4名同學相約進行羽毛球比賽.
(1)如果將4名同學隨機分成兩組進行對打,求恰好選中甲乙兩人對打的概率;
(2)如果確定由丁擔任裁判,用“手心、手背”的方法在另三人中競選兩人進行比賽.競選規則是:三人同時伸出“手心”或“手背”中的一種手勢,如果恰好只有兩人伸出的手勢相同,那么這兩人上場,否則重新競選.這三人伸出“手心”或“手背”都是隨機的,求一次競選就能確定甲、乙進行比賽的概率.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:![]() 列舉出將4名同學隨機分成兩組進行對打所有可能的結果,找出甲乙兩人對打的情況數,根據概率公式計算即可.
列舉出將4名同學隨機分成兩組進行對打所有可能的結果,找出甲乙兩人對打的情況數,根據概率公式計算即可.
![]() 畫樹狀圖寫出所有的情況,根據概率的求法計算概率.
畫樹狀圖寫出所有的情況,根據概率的求法計算概率.
詳解:(1)甲同學能和另一個同學對打的情況有三種:
(甲、乙),(甲、丙),(甲、丁)
則恰好選中甲乙兩人對打的概率為:![]()
(2)樹狀圖如下:
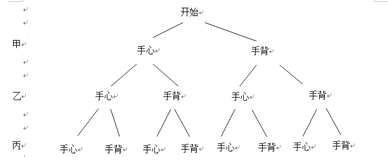
一共有8種等可能的情況,其中能確定甲乙比賽的可能為(手心、手心、手背)、(手背、手背、手心)兩種情況,因此,一次競選就能確定甲、乙進行比賽的概率為![]() .
.
點睛:考查概率的計算,明確概率的意義時解題的關鍵,概率等于所求情況數與總情況數的比.
【題型】解答題
【結束】
22
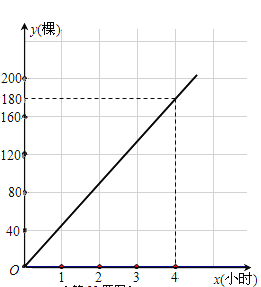
【題目】為了“綠化環境,美化家園”,3月12日(植樹節)上午8點,某校901、902班同學同時參加義務植樹.901班同學始終以同一速度種植樹苗,種植樹苗的棵數y1與種植時間x(小時)的函數圖象如圖所示;902班同學開始以1小時種植40棵的速度工作了1.5小時后,因需更換工具而停下休息半小時,更換工具后種植速度提高至原來的1.5倍.
(1)求902班同學上午11點時種植的樹苗棵數;
(2)分別求出901班種植數量y1、902班種植數量y2與種植時間x(小時)之間的函數關系式,并在所給坐標系上畫出y2關于x的函數圖象;
(3)已知購買樹苗不多于120棵時,每棵樹苗的價格是20元;購買樹苗超過120棵時,超過的部分每棵價格17元.若本次植樹所購樹苗的平均成本是18元,則兩班同學上午幾點可以共同完成本次植樹任務?
查看答案和解析>>
科目:初中數學 來源: 題型:
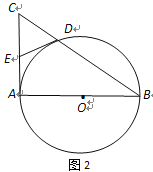
【題目】已知AB是⊙O的直徑,AC是⊙O的切線,BC交⊙O于點D(如圖1).
(1)若AB=2,∠B=30°,求CD的長;
(2) 取AC的中點E,連結D、E(如圖2),求證:DE與⊙O相切.

【答案】(1)![]() ;(2)見解析
;(2)見解析
【解析】分析:![]() 連接AD ,根據AC是⊙O的切線,AB是⊙O的直徑,得到∠CAB=∠ADB=90°,根據∠B=30°,解直角三角形求得
連接AD ,根據AC是⊙O的切線,AB是⊙O的直徑,得到∠CAB=∠ADB=90°,根據∠B=30°,解直角三角形求得![]() 的長度.
的長度.
![]() 連接OD,AD.根據DE=CE=EA,∠EDA=∠EAD. 根據OD=OA,得到
連接OD,AD.根據DE=CE=EA,∠EDA=∠EAD. 根據OD=OA,得到
∠ODA=∠DAO,得到∠EDA+∠ODA=∠EAD+∠DAO.得到∠EDO=90°即可.
詳解:(1)如圖,連接AD ,
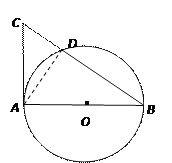
∵AC是⊙O的切線,AB是⊙O的直徑,
∴∠CAB=∠ADB=90°,
∴ΔCAB,ΔCAD均是直角三角形.
∴∠CAD=∠B=30°.
在RtΔCAB中,AC=ABtan30°=![]()
∴在RtΔCAD中,CD=ACsin30°=![]()
(2)如圖,連接OD,AD.

∵AC是⊙O的切線,AB是⊙O的直徑,
∴∠CAB=∠ADB=∠ADC=90°,
又∵E為AC中點,
∴DE=CE=EA,
∴∠EDA=∠EAD.
∵OD=OA,
∴∠ODA=∠DAO,
∴∠EDA+∠ODA=∠EAD+∠DAO.
即:∠EDO=∠EAO=90°.
又點D在⊙O上,因此DE與⊙O相切.
點睛:考查解直角三角形,圓周角定理,切線的判定與性質等,屬于圓的綜合題,比較基礎.注意切線的證明方法,是高頻考點.
【題型】解答題
【結束】
21
【題目】課外活動時間,甲、乙、丙、丁4名同學相約進行羽毛球比賽.
(1)如果將4名同學隨機分成兩組進行對打,求恰好選中甲乙兩人對打的概率;
(2)如果確定由丁擔任裁判,用“手心、手背”的方法在另三人中競選兩人進行比賽.競選規則是:三人同時伸出“手心”或“手背”中的一種手勢,如果恰好只有兩人伸出的手勢相同,那么這兩人上場,否則重新競選.這三人伸出“手心”或“手背”都是隨機的,求一次競選就能確定甲、乙進行比賽的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把2018個正整數1,2,3,4,…,2018按如圖方式排列成一個表.

(1)用如圖方式框住表中任意4個數,記左上角的一個數為![]() ,則另三個數用含
,則另三個數用含![]() 的式子表示出來,從小到大依次是__________、___________、_______________(請直接填寫答案);
的式子表示出來,從小到大依次是__________、___________、_______________(請直接填寫答案);
(2)用(1)中方式被框住的4個數之和可能等于2019嗎?如果可能,請求出![]() 的值;如果不可能,請說明理由.
的值;如果不可能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
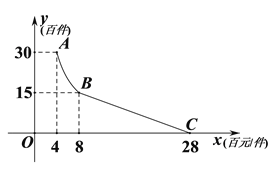
【題目】2017年元旦莫小貝在襄陽萬達廣場購進一家商鋪,裝修后用于銷售某品牌的女裝.2018元旦莫小貝盤點時發現:2017年自家店內女裝的平均成本為4百元/件,當年的銷售量![]() (百件)與平均銷售價格
(百件)與平均銷售價格![]() (百元/件)的關系如圖所示,其中AB為反比例函數圖象的一部分,BC為一次函數圖象的一部分.
(百元/件)的關系如圖所示,其中AB為反比例函數圖象的一部分,BC為一次函數圖象的一部分.
(1)請求出![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(2)若莫小貝購商鋪及裝修一共花了120萬元,請通過計算說明2017年莫小貝是賺還是虧?若賺,最多賺多少元?若虧,最少虧多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,小賢為了體驗四邊形的不穩定性,將四根木條用釘子釘成一個矩形框架ABCD,B與D兩點之間用一根橡皮筋拉直固定,然后向右扭動框架,觀察所得四邊形的變化,下列判斷錯誤的是( )
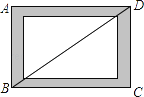
A. 四邊形ABCD由矩形變為平行四邊形 B. BD的長度增大
C. 四邊形ABCD的面積不變 D. 四邊形ABCD的周長不變
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com