
【題目】(本題滿分12分)
如圖,在△ABC中,BA=BC=20cm,AC=30cm,點P從A點出發,沿著AB以每秒4cm的速度向B點運動;同時點Q從C點出發,沿CA以每秒3cm的速度向A點運動,設運動時間為x秒.
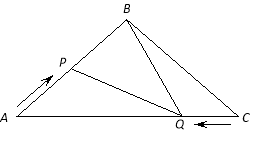
(1)、當x為何值時,PQ∥BC;
(2)、是否存在某一時刻,使△APQ∽△CQB,若存在,求出此時AP的長;若不存在,請說理由;
(3)、當![]() 時,求
時,求![]() 的值.
的值.
【答案】(1)、x=![]() ;(2)、AP=
;(2)、AP=![]() ;(3)、
;(3)、![]() .
.
【解析】
試題分析:(1)、根據PQ∥BC可得△APQ∽△ABC,從而求出x的值;(2)、根據相似三角形的性質可得![]() ,然后求出x的值;(3)、根據三角形的面積之比得出CQ:AC=1:3,根據AC的長度求出CQ的長度,然后計算出x的值,然后求出AP:AB的值,從而得出三角形的比值.
,然后求出x的值;(3)、根據三角形的面積之比得出CQ:AC=1:3,根據AC的長度求出CQ的長度,然后計算出x的值,然后求出AP:AB的值,從而得出三角形的比值.
試題解析:(1)、由題意知 AP=4x,CQ=3x若PQ∥BC 則△APQ∽△ABC
![]() ∵AB=BC=20 AC=30 ∴AQ=30―3x
∵AB=BC=20 AC=30 ∴AQ=30―3x
∴![]() ∴
∴![]() ∴當
∴當![]() 時,PQ∥BC.
時,PQ∥BC.
(2)、存在
∵△APQ∽△CQB 則![]() ∴
∴![]()
∴![]() ∴
∴![]() .
. ![]() .
.
∴當AP的長為![]() 時,△APQ∽△CQB
時,△APQ∽△CQB
(3)、∵![]() ∴
∴![]() 又∵AC=30 ∴CQ=10
又∵AC=30 ∴CQ=10
即![]()
![]() 此時,
此時,![]()
∴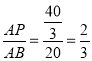 ∴
∴![]()


 智能訓練練測考系列答案
智能訓練練測考系列答案 計算高手系列答案
計算高手系列答案科目:初中數學 來源: 題型:
【題目】(1)如圖①,一個無蓋的長方體盒子的棱長分別為![]() ,
,![]() ,
,![]() ,盒子的內部頂點
,盒子的內部頂點![]() 處有一只昆蟲甲,在盒子的內部頂點
處有一只昆蟲甲,在盒子的內部頂點![]() 處有一只昆蟲乙(盒壁的厚度忽略不計)假設昆蟲甲在頂點
處有一只昆蟲乙(盒壁的厚度忽略不計)假設昆蟲甲在頂點![]() 處靜止不動,請計算
處靜止不動,請計算![]() 處的昆蟲乙沿盒子內壁爬行到昆蟲甲
處的昆蟲乙沿盒子內壁爬行到昆蟲甲![]() 處的最短路程,并畫出其最短路徑,簡要說明畫法
處的最短路程,并畫出其最短路徑,簡要說明畫法
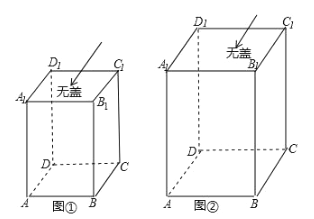
(2)如果(1)問中的長方體的棱長分別為![]() ,
,![]() ,如圖②,假
,如圖②,假
設昆蟲甲從盒內頂點![]() 以1厘米/秒的速度在盒子的內部沿棱
以1厘米/秒的速度在盒子的內部沿棱![]() 向下爬行,同時昆蟲乙從
向下爬行,同時昆蟲乙從
盒內頂點![]() 以3厘米/秒的速度在盒壁的側面上爬行,那么昆蟲乙至少需要多長時間才能捕
以3厘米/秒的速度在盒壁的側面上爬行,那么昆蟲乙至少需要多長時間才能捕
捉到昆蟲甲?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】操場上有一根豎直立在地面上的旗桿,繩子自然下垂到地面還剩余2米,當把繩子拉開8米后,繩子剛好斜著拉直下端接觸地面(如圖①)
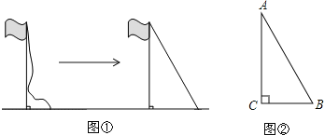
(1)請根據你的閱讀理解,將題目的條件補充完整:如圖②,Rt△ABC中 ∠C=90°,BC=8米,____________________________.求AC的長.
(2)根據(1)中的條件,求出旗桿的高度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com