
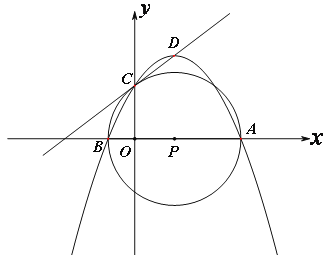
【題目】如圖,在平面直角坐標系中,拋物線y=![]() x2+bx+c經過點A(4,0)、B(-1,0),與y軸交于點C,D為拋物線的頂點,過A、B、C 作⊙P.
x2+bx+c經過點A(4,0)、B(-1,0),與y軸交于點C,D為拋物線的頂點,過A、B、C 作⊙P.
(1)求b、c的值;
(2)求證:線段AB是⊙P的直徑;
(3)連接AC,AD,在坐標平面內是否存在點Q,使得△CDA~△CPQ,若存在,求出點Q的坐標,若不存在,請說明理由。
【答案】(1) ![]() ;(2)證明見解析;(3)Q1(-
;(2)證明見解析;(3)Q1(-![]() ,-
,-![]() ),Q2(
),Q2(![]() ,
,![]() ).
).
【解析】
試題分析:(1)用待定系數法求出拋物線的系數b,c;
(2)先求出點C(0,2),再根據A(4,0)、B(-1,0),求出AC2,BC2,AB2,用勾股定理逆定理說明△ABC是直角三角形即可;
(3)先求出線段AC,AD,CD,CP,根據三角形相似得到比例式,再設出點Q的坐標建立方程求解.
試題解析:(1)∵拋物線y=-![]() x2+bx+c經過點A(4,0)、B(-1,0),
x2+bx+c經過點A(4,0)、B(-1,0),
∴ ,
,
∴![]()
(2)由(1)可知拋物線的解析式為:y=-![]() x2+
x2+![]() x+2,C(0,2),
x+2,C(0,2),
∵A(4,0)、B(-1,0),
∴BC2=OB2+OC2=1+4=5,AC2=OA2+OC2=16+4=20,AB2=25,
∴BC2+AC2=AB2,
∴∠ACB=90°,
∴線段AB是⊙P的直徑;
(3)由(1)可知拋物線的解析式為:y=-![]() x2+
x2+![]() x+2,
x+2,
∴D(![]() ,
,![]() ),
),
∵A(4,0),C(0,2),
∴AC=2![]() ,AD=
,AD=![]() ,CD=
,CD=![]() ,
,
∵P(![]() ,0),
,0),
∴CP=![]() ,
,
∵△CDA∽△CPQ,
∴![]()
∴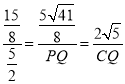 ,
,
∴PQ=![]() ,CQ=
,CQ=![]() ,
,
設點Q(m,n),
∴PQ=![]() =
=![]() ,
,
CQ=![]() =
=![]() ,
,
∴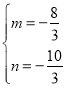 或
或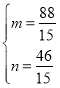 ,
,
∴Q1(-![]() ,-
,-![]() ),Q2(
),Q2(![]() ,
,![]() ).
).


科目:初中數學 來源: 題型:
【題目】小明在學習了正方形之后,給同桌小文出了道題,從下列四個條件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中選兩個作為補充條件,使ABCD為正方形(如圖),現有下列四種選法,你認為其中錯誤的是( )
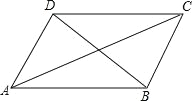
A.①② B.②③ C.①③ D.②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,BC的垂直平分線EF交∠ABC的平分線BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )

A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
科目:初中數學 來源: 題型:
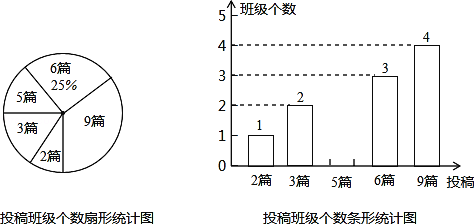
【題目】為積極響應市委,市政府提出的“實現偉大中國夢,建設美麗新城市”的號召,我市某校在八,九年級開展征文活動,校學生會對這兩個年級各班內的投稿情況進行統計,并制成了如圖所示的兩幅不完整的統計圖.
(1)求扇形統計圖中投稿篇數為2所對應的扇形的圓心角的度數:
(2)求該校八,九年級各班在這一周內投稿的平均篇數,并將該條形統計圖補充完整.
(3)在投稿篇數為9篇的兩個班級中,八,九年級各有兩個班,校學生會準備從這四個中選出兩個班參加全市的表彰會,請你用列表法或畫樹狀圖的方法求出所選兩個班正好不在同一年級的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com