
已如:矩形ABCD中,![]() ,點M在對角線AC上,直線
,點M在對角線AC上,直線![]() 過點M且與AC垂直,與AD相交于點E。
過點M且與AC垂直,與AD相交于點E。
(1)如果直線![]() 與邊BC相交于H(如圖1),
與邊BC相交于H(如圖1),![]() ,且
,且![]() ,求AE的長;(用含
,求AE的長;(用含![]() 的代數式表示)
的代數式表示)
(2)在(1)中,又直線![]() 把矩形分成兩部分的面積比為25,求
把矩形分成兩部分的面積比為25,求![]() 的值;
的值;
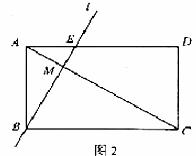
(3)若![]() ,且直線
,且直線![]() 經過點B(如圖2),求AD的長;
經過點B(如圖2),求AD的長;
(4)如果直線![]() 分別與邊AD、AB相交于點E、F,
分別與邊AD、AB相交于點E、F,![]() 。設AD長為
。設AD長為![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 與
與![]() 的函數關系式,并指出
的函數關系式,并指出![]() 的取值范圍。(求
的取值范圍。(求![]() 的取值范圍可不寫過程)
的取值范圍可不寫過程)
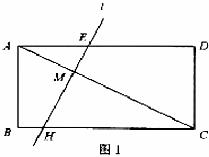
解:( 1 )∵在矩形ABCD 中.∠D = 90º, ![]()
∴![]() ,
,![]()
∵![]() ,
,![]() ,
,
∴![]() ∽
∽![]()
∴![]() ,
,
∴ ,
,
( 2 ) (法一)
∵AD∥BC,易得![]() ∽
∽![]() ,
,
∴![]()
∴![]() ,∴
,∴![]()
∴梯形面積![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() (負值舍去,經檢驗是原方程的解)
(負值舍去,經檢驗是原方程的解)
(法二)∵由(1)得![]() ,∴
,∴![]()
∵AD∥BC,易得![]() ∽
∽![]()
∴![]()
∴![]() ,∴
,∴![]()
∵![]() ,∴
,∴
( 3 ) (法一)與(1)、(2)同理得![]() ,
,![]() ,
,
∴![]()
∴![]() ,
,
∵直線![]() 過點B,∴
過點B,∴![]()
∴![]() ,∴
,∴![]() (負值舍去,經檢驗是原方程的解)
(負值舍去,經檢驗是原方程的解)
(法二)連結BD交AC于點O,則![]()
又∵![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]()
∴![]() 是等邊三角形,
是等邊三角形,
∵![]() ,∴
,∴![]() ∴
∴![]() 。
。
( 4 )
(法一)在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,
,![]() ,
,
由![]() ∽
∽![]() ,有:
,有:![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]()
∴![]() ,又∵
,又∵![]()
∴![]() ∽
∽![]() ,∴
,∴![]()
∴ ,∴
,∴![]() ,
,
∴![]() 與
與![]() 的函數關系式是
的函數關系式是![]() 。
。
(法二)在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,
,![]() ,
,
由![]() ∽
∽![]() ,有:
,有:![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]()
∴![]() ,又∵
,又∵![]()
∴![]() ∽
∽![]() ,
,![]() ∴
∴![]() ,
,
∴![]()
∴![]() 與
與![]() 的函數關系式是
的函數關系式是![]()


科目:初中數學 來源: 題型:
 ,E,F三點共線時,兩點同時停止運動.設點E移動的時間為t(秒).
,E,F三點共線時,兩點同時停止運動.設點E移動的時間為t(秒).查看答案和解析>>
科目:初中數學 來源: 題型:
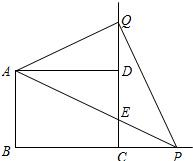 如圖,已知在矩形ABCD中,AB=3,BC=4,P是邊BC延長線上的一點,連接AP交邊CD于點E,把射線AP沿直線AD翻折,交射線CD于點Q,設CP=x,DQ=y.
如圖,已知在矩形ABCD中,AB=3,BC=4,P是邊BC延長線上的一點,連接AP交邊CD于點E,把射線AP沿直線AD翻折,交射線CD于點Q,設CP=x,DQ=y.查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com