
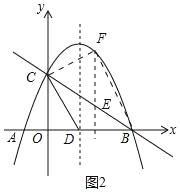
【題目】如圖,拋物線y=![]() +bx+c與x軸交于A、B兩點,與y軸交于點C,拋物線的對稱軸交x軸于點D,已知A(﹣1,0),C(0,2).
+bx+c與x軸交于A、B兩點,與y軸交于點C,拋物線的對稱軸交x軸于點D,已知A(﹣1,0),C(0,2).
(1)求拋物線的解析式;
(2)在拋物線的對稱軸上是否存在點P,使△PCD是以CD為腰的等腰三角形?如果存在,直接寫出P點的坐標;如果不存在,請說明理由;
(3)點E是線段BC上的一個動點,過點E作x軸的垂線與拋物線相交于點F,當點E運動到什么位置時,△CBF的面積最大?求出△CBF的最大面積及此時E點的坐標.

【答案】(1)y=![]() +
+![]() x+2;(2)存在.P(
x+2;(2)存在.P(![]() ,4)或(
,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(3) 當E運動到BC的中點時,△EBC面積最大,△EBC最大面積是4,此時E(2,1).
);(3) 當E運動到BC的中點時,△EBC面積最大,△EBC最大面積是4,此時E(2,1).
【解析】
試題分析:(1)把A(﹣1,0),C(0,2)代入y=![]() +bx+c列方程組即可;
+bx+c列方程組即可;
(2)先求出CD的長,分兩種情形①當CP=CD時,②當DC=DP時分別求解即可;
(3)求出直線BC的解析式,設E(m,![]() ),則F(m,
),則F(m,![]() ),構建二次函數,利用二次函數的性質即可解決問題.
),構建二次函數,利用二次函數的性質即可解決問題.
試題解析:(1)把A(﹣1,0),C(0,2)代入y=![]() +bx+c得
+bx+c得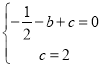 ,
,
解得b=![]() ,c=2,
,c=2,
∴拋物線的解析式為y=![]() +
+![]() x+2;
x+2;
(2)存在.如圖1中,∵C(0,2),D(![]() ,0),
,0),
∴OC=2,OD=![]() ,CD=
,CD=![]() =
=![]() ,
,

①當CP=CD時,可得![]() (
(![]() ,4),
,4),
②當DC=DP時,可得![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() ),
),
綜上所述,滿足條件的P點的坐標為(![]() ,4)或(
,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
(3)如圖2中,
對于拋物線y=![]() +
+![]() x+2,當y=0時,
x+2,當y=0時,![]() +
+![]() x+2=0,解得
x+2=0,解得![]() =4,
=4,![]() =﹣1,
=﹣1,
∴B(4,0),A(﹣1,0),
由B(4,0),C(0,2)得直線BC的解析式為y=![]() x+2,
x+2,
設E(m,![]() ),則F(m,
),則F(m,![]() ),
),
EF=(![]() )﹣(
)﹣(![]() )=
)=![]() =
=![]() ,
,
∴![]() <0,∴當m=2時,EF有最大值2,
<0,∴當m=2時,EF有最大值2,
此時E是BC中點,
∴當E運動到BC的中點時,△EBC面積最大,
∴△EBC最大面積=![]() ×4×EF=
×4×EF=![]() ×4×2=4,此時E(2,1).
×4×2=4,此時E(2,1).


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:初中數學 來源: 題型:
【題目】在下列各式中,應填入“(-y)”的是( )
A. -y3·______=-y4 B. 2y3·______=-2y4
C. (-2y)3·______=-8y4 D. (-y)12·______=-3y13
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列式子(1)2x﹣7≥﹣3,(2)![]() ﹣x>0,(3)7<9,(4)x2+3x>1,(5)
﹣x>0,(3)7<9,(4)x2+3x>1,(5)![]() ﹣2(a+1)≤1,(6)m﹣n>3,中是一元一次不等式的有( )
﹣2(a+1)≤1,(6)m﹣n>3,中是一元一次不等式的有( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】食品安全是關乎民生的重要問題,在食品中添加過量的添加劑對人體健康有害,但適量的添加劑對人體健康無害而且有利于食品的儲存和運輸.為提高質量,做進一步研究,某飲料加工廠需生產A、B兩種飲料共100瓶,需加入同種添加劑270克,其中A飲料每瓶需加添加劑2克,B飲料每瓶需加添加劑3克,飲料加工廠生產了A、B兩種飲料各多少瓶?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com