
【題目】如圖(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足為D。AF平分∠CAB,交CD于點E,交CB于點F。

(1)求證:CE=CF。
(2)將圖(1)中的△ADE沿AB向右平移到△A′D′E′的位置,使點E′落在BC邊上,其它條件不變,如圖(2)所示。試猜想:BE′與CF有怎樣的數量關系?請證明你的結論。
【答案】(1)見解析證明;(2)![]() =CF.理由見解析證明.
=CF.理由見解析證明.
【解析】
試題分析:(1)根據角平分線的定義可得∠CAF=∠EAD,再根據等角的余角相等求出∠CFA=∠AED ,然后根據對頂角相等可得∠AED=∠CEF,從而得到∠CFA=∠AED,再根據等角對等邊證明即可;(2)過點E作EG⊥AC于點G,根據角平分線的性質得到ED=EG,根據平移的性質可得![]() =DE,然后求出∠ACD=∠B,再利用“角角邊”證明△CEG≌
=DE,然后求出∠ACD=∠B,再利用“角角邊”證明△CEG≌![]() 全等,根據全等三角形對應邊相等可得BE′=CE,從而得到BE′=CF.
全等,根據全等三角形對應邊相等可得BE′=CE,從而得到BE′=CF.
試題解析:(1)∵AF平分∠CAB,∴∠CAF=∠EAD,∵∠ACB=90°,∴∠CAF+∠CFA=90°,∵CD⊥AB,∴∠EAD+∠AED=90°, ∴∠CFA=∠AED ,又∵∠AED=∠CEF,∴∠CFA=∠AED,∴CE=CF;
(2)答:![]() =CF. 過點E作EG⊥AC于點G,
=CF. 過點E作EG⊥AC于點G,
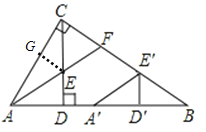
∵AF平分∠CAB,ED⊥AB,EG⊥AC,∴ED=EG,∵△ADE平移得到![]() ,∴
,∴![]() =DE,∴
=DE,∴![]() =GE,∵∠ACB=90°,∴∠ACD+∠DCB=90°,∵CD⊥AB,∴∠B+∠DCB=90°,∴∠ACD=∠B,在△CEG和
=GE,∵∠ACB=90°,∴∠ACD+∠DCB=90°,∵CD⊥AB,∴∠B+∠DCB=90°,∴∠ACD=∠B,在△CEG和![]() 中,∵
中,∵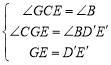 ,∴△CEG≌
,∴△CEG≌![]() (AAS),∴CE=
(AAS),∴CE=![]() ,又∵CE=CF,∴
,又∵CE=CF,∴![]() =CF.
=CF.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】已知,點O是直線AB上一點,OC、OD為從點O引出的兩條射線,∠BOD=30°,∠COD=![]() ∠AOC.
∠AOC.
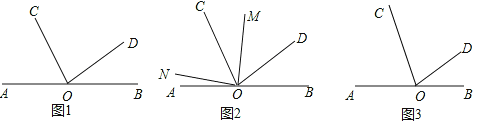
(1)如圖①,求∠AOC的度數;
(2)如圖②,在∠AOD的內部作∠MON=90°,請直接寫出∠AON與∠COM之間的數量關系 ;
(3)在(2)的條件下,若OM為∠BOC的角平分線,試說明∠AON=∠CON.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,射線OA的方向是北偏東20°,射線OB的方向是北偏西40°,OD是OB的反向延長線.若OC是∠AOD的平分線,則∠BOC=_____°,射線OC的方向是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一組數,按照下列規律排列:
1,
2,3,
6,5,4,
7,8,9,10,
15,14,13,12,11,
16,17,18,19,20,21,
……
數字5在第三行左數第二個,我們用(3,2)點示5的位置,那點這組成數里的數字100的位置可以表示為( )
A. (14,9) B. (14,10) C. (14,11) D. (14,12)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,由12個形狀、大小完全相同的小矩形組成一個大的矩形網格,小矩形的頂點稱為這個矩形網格的格點,已知這個大矩形網格的寬為4,△ABC的頂點都在格點.
(1)求每個小矩形的長與寬;
(2)在矩形網格中找出所有的格點E,使△ABE為直角三角形;(描出相應的點,并分別用E1 , E2…表示)
(3)求sin∠ACB的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的兩條高線BD,CE相交于點F,已知∠ABC=60°,AB=10,CF=EF,則△ABC的面積為( ) 
A.20 ![]()
B.25 ![]()
C.30 ![]()
D.40 ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,以AB為直徑的⊙O分別交AC,BC于點D,E,點F在AC的延長線上,且AC=CF,∠CBF=∠CFB. 
(1)求證:直線BF是⊙O的切線;
(2)若點D,點E分別是弧AB的三等分點,當AD=5時,求BF的長和扇形DOE的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com