日韩视频三区,国内精品久久久久久,一区二区福利

<del id="6ecyq"></del>

<ul id="6ecyq"></ul>

精英家教網(wǎng) > 初中數(shù)學 > 題目詳情

【題目】若點P（a+4，﹣5﹣b）與點Q（2b，2a+8）關(guān)于原點成中心對稱，a+b2 =___.

【答案】-1

【解析】

根據(jù)點P（a+4，﹣5﹣b）與點Q（2b，2a+8）關(guān)于原點成中心對稱，可得a=-2，b=-1，然后把a、b的值代入，求出a+b2的值為多少即可．

解：∵點P（a+4，﹣5﹣b）與點Q（2b，2a+8）關(guān)于原點對稱，
∴a+4=-2b，-5-b=-（2a+8），
解得：a=-2，b=-1，
則a+b2=-2+1=-1．
故答案為-1．

練習冊系列答案

自主創(chuàng)新作業(yè)系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關(guān)習題

科目：初中數(shù)學 來源： 題型：

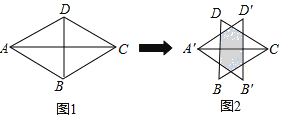
【題目】如圖，兩個等邊△ABD，△CBD的邊長均為1，將△ABD沿AC方向向右平移到△A′B′D′的位置，得到圖2，則陰影部分的周長為（）

A．1 B．2 C．2.5 D．3

查看答案和解析>>

科目：初中數(shù)學 來源： 題型：

【題目】下列運算中正確的是（　　）

A. b3b3=2b3 B. x2x3=x6 C. （a5）2=a7 D. a5÷a2=a3

查看答案和解析>>

科目：初中數(shù)學 來源： 題型：

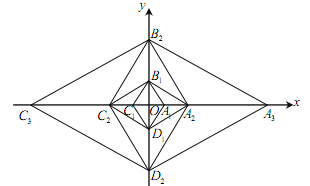
【題目】（成都）已知菱形的邊長為2，=60°，對角線，相交于點O．以點O為坐標原點，分別以，所在直線為x軸、y軸，建立如圖所示的直角坐標系．以為對角線作菱形∽菱形，再以為對角線作菱形∽菱形，再以為對角線作菱形∽菱形，，按此規(guī)律繼續(xù)作下去，在x軸的正半軸上得到點，，，．．．．．．，，則點的坐標為________．

查看答案和解析>>

科目：初中數(shù)學 來源： 題型：

【題目】在下列條件中，①∠A+∠B=∠C； ②∠A：∠B：∠C=1：2：3； ③∠A= ∠B= ∠C； ④∠A=∠B=2∠C； ⑤∠A=2∠B=3∠C，能確定△ABC為直角三角形的條件有（）
A.2個
B.3個
C.4個
D.5個

查看答案和解析>>

科目：初中數(shù)學 來源： 題型：

【題目】如圖，ABCD的對角線AC、BD相交于點O，AE=CF．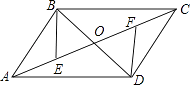

（1）求證：△BOE≌△DOF；
（2）連接DE、BF，若BD⊥EF，試探究四邊形EBDF的形狀，并對結(jié)論給予證明．

查看答案和解析>>

科目：初中數(shù)學 來源： 題型：

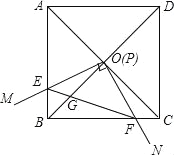
【題目】如圖，邊長為1的正方形ABCD的對角線AC、BD相交于點O．有直角∠MPN，使直角頂點P與點O重合，直角邊PM、PN分別與OA、OB重合，然后逆時針旋轉(zhuǎn)∠MPN，旋轉(zhuǎn)角為θ（0°＜θ＜90°），PM、PN分別交AB、BC于E、F兩點，連接EF交OB于點G，則下列結(jié)論中正確的是．

（1）EF=OE；（2）S四邊形OEBF：S正方形ABCD=1：4；（3）BE+BF=OA；（4）在旋轉(zhuǎn)過程中，當△BEF與△COF的面積之和最大時，AE=；（5）OGBD=AE2+CF2．