
【題目】如圖,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,動點P從點C出發,按C→B→A的路徑,以2cm每秒的速度運動,設運動時間為t秒,當t為時,△ACP是等腰三角形. 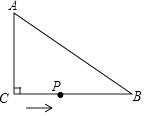
【答案】3或6或6.5或5.4
【解析】解:∵AC=6,BC=8, ∴由勾股定理可知:AB=10,
當點P在CB上運動時,
由于∠ACP=90°,
∴只能有AC=CP,如圖1,
∴CP=6,
∴t= ![]() =3,
=3,
當點P在AB上運動時,①AC=AP時,如圖2,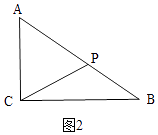
∴AP=6,PB=AB﹣CP=10﹣6=4,
∴t= ![]() =6,②當AP=CP時,如圖3,
=6,②當AP=CP時,如圖3,
此時點P在線段AC的垂直平分線上,
過點P作PD⊥AC于點D,
∴CD= ![]() AC=3,PD是△ACB的中位線,
AC=3,PD是△ACB的中位線,
∴PD= ![]() BC=4,
BC=4,
∴由勾股定理可知:AP=5,
∴PB=5,
∴t= ![]() =6.5;③AC=PC時,如圖4,
=6.5;③AC=PC時,如圖4,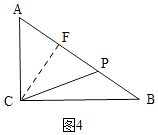
過點C作CF⊥AB于點F,
∴cos∠A= ![]() =
= ![]() ,
,
∴AF=3.6,
∴AP=2AF=7.2,
∴PB=10﹣7.2=2.8,
∴t= ![]() =5.4;
=5.4;
綜上所述,當t為3或6或6.5或5.4時,△ACP是等腰三角形.
故答案為:3或6或6.5或5.4.
由于沒有說明哪一條邊是腰,故需要分情況討論.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:初中數學 來源: 題型:
【題目】已知一次函數y=kx+7的圖像經過點A(2,3).
(1)求k的值;
(2)判斷點B(-1,8),C(3,1)是否在這個函數的圖像上,并說明理由;
(3)當-3<x<-1時,求y的取值范圍.
【答案】(1)k=-2(2)點B不在,點C在,(3)9<y<13
【解析】
試題分析:(1)把點A(2,3)代入y=kx+7即可求出k的值;(2)點B(-1,8),C(3,1)的橫坐標代入函數解析式驗證即可;(3)根據x的取值范圍,即可求出y的取值范圍.
試題解析:(1)把點A(2,3)代入y=kx+7得:k=-2
(2)當x=-1時,y=-2×(-1)+7=9
∵9≠8∴點B不在拋物線上.
當x=3時,y=-2×3+7=1
∴點C在拋物線上
(3)當x=-3時,y=13,當x=-,1時,y=9,所以9<y<13
考點:一次函數.
【題型】解答題
【結束】
24
【題目】順豐快遞公司派甲、乙兩車從A地將一批物品勻速運往B地,甲出發0.5h后乙開始出發,結果比甲早1(h)到達B地,如圖,線段OP、MN分別表示甲、乙兩車離A地的距離S(km)與時間t(h)的關系,a表示A、B兩地之間的距離.請結合圖中的信息解決如下問題:

(1)分別計算甲、乙兩車的速度及a的值;
(2)乙車到達B地后以原速立即返回,請問甲車到達B地后以多大的速度立即勻速返回,才能與乙車同時回到A地?并在圖中畫出甲、乙兩車在返回過程中離A地的距離S(km)與時間t(h)的函數圖象.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數y1=kx+b的圖像經過點(0,-2),(2,2).
(1)求一次函數的表達式,并在所給直角坐標系中畫出此函數的圖像;;
(2)根據圖像回答:當x 時,y1=0;
(3)求直線y1=kx+b、直線y2=-2x+4與y軸圍成的三角形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,E、F分別是邊AD、CD上的點,AE=ED,DF=![]() DC,連接EF并延長交BC的延長線于點G。
DC,連接EF并延長交BC的延長線于點G。
(1)求證:△ABE∽△DEF;
(2)若正方形的邊長為4,求BG的長。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】校園安全與每個師生、家長和社會有著切身的關系.某校教學樓共五層,設有左、右兩個樓梯口,通常在放學時,若持續不正常,會導致等待通過的人較多,發生擁堵,從而出現不安全因素.通過觀察發現位于教學樓二、三樓的七年級學生從放學時刻起,經過單個樓梯口等待人數按每分鐘12人遞增,6分鐘后經過單個樓梯口等待人數按每分鐘12人遞減;位于四、五樓的八年級學生從放學時刻起,經過單個樓梯口等待人數y2與時間為t(分)滿足關系式y2=﹣4t2+48t﹣96(0≤t≤12).若在單個樓梯口等待人數超過80人,就會出現安全隱患.
(1)試寫出七年級學生在單個樓梯口等待的人數y1(人)和從放學時刻起的時間t(分)之間的函數關系式,并指出t的取值范圍.
(2)若七、八年級學生同時放學,試計算等待人數超過80人所持續的時間.
(3)為了避免出現安全隱患,該校采取讓七年級學生提前放學措施,要使單個樓梯口等待人數不超過80人,則七年級學生至少比八年級提前幾分鐘放學?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等邊三角形的頂點A(1,1)、B(3,1),規定把等邊△ABC“先沿x軸翻折,再向左平移1個單位”為一次変換,如果這樣連續經過2016次變換后,等邊△ABC的頂點C的坐標為________________________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以∠AOB的頂點O為圓心,適當長為半徑畫弧,交OA于點C,交OB于點D.再分別以點C、D為圓心,大于![]() CD的長為半徑畫弧,兩弧在∠AOB內部交于點E,過點E作射線OE,連接CD.則下列說法錯誤的是
CD的長為半徑畫弧,兩弧在∠AOB內部交于點E,過點E作射線OE,連接CD.則下列說法錯誤的是

A.射線OE是∠AOB的平分線
B.△COD是等腰三角形
C.C、D兩點關于OE所在直線對稱
D.O、E兩點關于CD所在直線對稱
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 如圖,△ABC中,AB=AC,∠BAC=90°,點D是直線AB上的一動點(不和A、B重合),BE⊥CD于E,交直線AC于F.
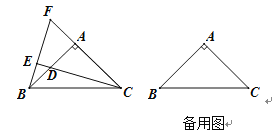
(1)點D在邊AB上時,試探究線段BD、AB和AF的數量關系,并證明你的結論;
(2)點D在AB的延長線或反向延長線上時,(1)中的結論是否成立?若不成立,請直接寫出正確結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某職業高中機電班共有學生42人,其中男生人數比女生人數的2倍少3人.
(1)該班男生和女生各有多少人?
(2)某工廠決定到該班招錄30名學生,經測試,該班男、女生每天能加工的零件數分別為50個和45個,為保證他們每天加工的零件總數不少于1460個,那么至少要招錄多少名男學生?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com